地震動シミュレーションデータの自動分類

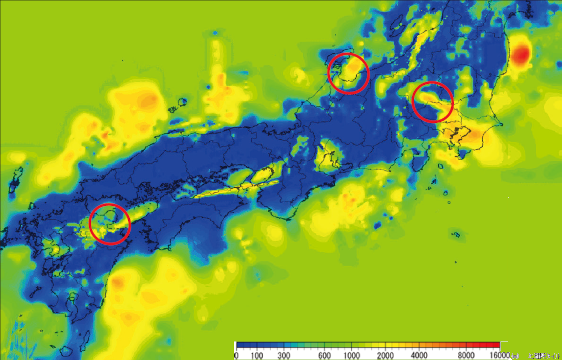
地震動シミュレーションデータの自動分類Automatic classification of the ground–motion simulation data赤木 翔＊　早川 俊彦＊　下野 五月＊Sho Akagi, Toshihiko Hayakawa, Satsuki Shimono近年、計算機の発達に伴い、多様な震源モデルを想定した多数の地震動シミュレーションが実行可能となった。防災・減災に利活用することを目的として、南海トラフや相模トラフにおける巨大海溝型地震のシミュレーションが実施され、結果が蓄積されている。我々は、これらのシミュレーションデータから地震動分布の推定手法の高度化等に活用できる情報を抽出することを目的として、膨大なシミュレーションデータを機械学習により自動的に分類する手法を開発した。本稿では南海トラフの地震動シミュレーションデータを例として、手法の適用結果と応用への展開について述べる。In recent years, many ground–motion simulations assuming various earthquake source models became possible with the development of computers. Many megathrust earthquakes on Nankai Trough or Sagami Trough are simulated for the purpose of utilizing for disaster prevention and disaster mitigation. We developed automatic classification methods for the big simulation data by machine learning methods to extract the information that improve the estimation methods for earthquake distribution. We describe the application results for Nankai Trough simulation data and the next deployment of the method. 1．まえがき近年、スーパーコンピュータを始めとする計算機の発達により、地震や津波を再現するシミュレーションを複数並行して高速に実行できるようになった。多様な断層の破壊過程を想定した地震の想定シナリオ（以下、地震シナリオ）に対して広範囲にわたる地震動シミュレーションが実施され、多数のシミュレーション結果が蓄積されている（例えば、参考文献⑴）。これらのシミュレーション結果には、防災上重要な地震ハザードの情報や地震動分布の推定手法の高度化に応用できるような地震動の性質等、防災・減災に広く利活用できる有用な情報が含まれている。しかし、１つの地震シナリオのシミュレーション結果は数万点に及ぶ評価地点で計算される地震動指標値からなるため、多数の地震シナリオに共通している性質や各評価地点での地震動の特徴を調査することは容易ではない。我々は、国立研究開発法人防災科学技術研究所（以下、防災科研）と協力し、地震動シミュレーションの結果から防災・減災に有用な情報を効率的に取り出すことを目的として膨大なシミュレーションデータを概観可能な程度の数のグループに自動的に分類する手法を開発した⑵。＊つくば事業部 第四技術部本稿では、面的に類似した地震動分布を持つ地震シナリオ同士を同一のグループに分類する手法と、多数の地震シナリオを通して類似した地震動が観測される評価地点同士を同一のグループに分類する手法の２つの手法を紹介する。２つの手法は共に、機械学習の代表的な手法である主成分分析とK–means法を組み合わせて構成した。本稿では南海トラフの巨大海溝型地震を想定した地震動シミュレーションデータを例として、２つの手法の適用結果とその特徴及び結果に対する考察を述べる。2．地震動シミュレーションデータ本稿で扱う南海トラフの地震動シミュレーションデータについてその概要を説明する。防災科研がパッケージ化した地震波伝播シミュレーションツールであるGMS⑶では、多様な震源モデルの破壊過程を表現するため、震源域、破壊開始点、浅部アスペリティ位置等が設定できる。防災科研では南海トラフの巨大海溝型地震を想定して計369個の地震シナリオの計算を実施した。震源域の計算パラメータとして、南海トラフ震源域全体を分割した計18個の小領域から15パターンの組み合わせを作成した。また、小領域の境界線の交点を10パターンの破壊開始点とした。南海トラフMSS技報・Vol.30 1震源域小領域破壊開始点18 17 16 15 14 13 7 1 9 8 2 3 10 4 11 5 12 6 4 2 6 3 1図１　南海トラフ地震シナリオの震源域の小領域と破壊開始点震源域の小領域と破壊開始点を図１に示す。図１で★は破壊開始点を表す。また、左図の丸囲み数字は震源域の小領域に対して、右図の四角囲みの数字は破壊開始点に対して割り振った番号をそれぞれ示している。地震動の評価範囲は九州地方、四国地方及び本州の東北地方南部までを含む範囲であり、計算結果を出力する評価地点の数は77,609 点にのぼる。𝑃 𝑃 𝑃 𝑃 𝑟 𝑟 𝑟 𝑟𝑃𝑃𝑃𝑃 = ∑ 𝜆𝜆𝜆𝜆𝑝𝑝𝑝𝑝 𝑀 𝑀 𝑀 𝑀 𝑝 𝑝 𝑝 𝑝=1 ∑ 𝜆𝜆𝜆𝜆𝑝𝑝𝑝𝑝 𝑝 𝑝 𝑝 𝑝=1 10 8 5 7 9 ⑵累積寄与率𝑟𝑟𝑟𝑟𝑃𝑃𝑃𝑃 が1.0に近いほど、次元削減により失われる情報量が少なくなる。3．基礎技術開発手法の基礎となる主成分分析とK–means法について概要を説明する。3.1　主成分分析主成分分析（例えば、参考文献⑷）は、𝑀𝑀𝑀𝑀 次元（𝑀𝑀𝑀𝑀>1 1）の入力データに対してデータをよく表現する𝑃𝑃𝑃𝑃 （≪𝑀𝑀𝑀𝑀 ）個の方向ベクトルを見つけ、データの各サンプルを𝑃𝑃𝑃𝑃 個の方向ベクトルで張る空間に射影することで次元削減されたデータを得る手法である。方向ベクトルは射影されたデータ点の分散が大きくなるように選ぶ。分散の大きさが𝑝𝑝𝑝𝑝 番目（𝑝𝑝𝑝𝑝 =1,2,…,𝑃𝑃𝑃𝑃 ）となる方向ベクトル𝒖𝒖𝒖𝒖𝑝𝑝𝑝𝑝∈ℝ𝑀𝑀𝑀𝑀 を第𝑝𝑝𝑝𝑝 主成分ベクトルと呼ぶ。𝑖𝑖𝑖𝑖 番目のサンプル𝒙 𝒙 𝒙 𝒙𝑖𝑖𝑖𝑖 ∈ ℝ𝑀𝑀𝑀𝑀 の第𝑝𝑝𝑝𝑝 主成分ベクトルへの射影𝛼𝛼𝛼𝛼𝑝𝑝𝑝𝑝 𝑖𝑖𝑖𝑖 を第𝑝𝑝𝑝𝑝 主成分スコアと呼ぶ。入力データの各サンプル𝒙𝒙𝒙𝒙𝑖𝑖𝑖𝑖 は、𝑝𝑝𝑝𝑝 番目までの主成分ベクトルの線形和で近似される。𝑃 𝑃 𝑃 𝑃 𝒙 𝒙 𝒙 𝒙𝑖𝑖𝑖𝑖 ≈ �𝛼𝛼𝛼𝛼𝑝𝑝𝑝𝑝 𝑖𝑖𝑖𝑖 ∗𝒖𝒖𝒖𝒖𝑝𝑝𝑝𝑝 𝑝 𝑝 𝑝 𝑝=1 ⑴元のデータをよく表現する次元𝑃𝑃𝑃𝑃 を決める方法として、累積寄与率による方法がある。寄与率とは、ある次元の分散を全ての次元の分散の総和で除算した値である。累積寄与率は第１次元からある次元までの寄与率の和であり、次元𝑝𝑝𝑝𝑝 の分散を𝜆𝜆𝜆𝜆𝑝𝑝𝑝𝑝 としたとき、次元𝑃𝑃𝑃𝑃 の累積寄与率𝑟𝑟𝑟𝑟𝑃𝑃𝑃𝑃 は以下の式で与えられる。入力データの各サンプルを𝑃𝑃𝑃𝑃 （≪𝑀𝑀𝑀𝑀 ）個の主成分スコアに変換することで、解析対象となるデータの次元が削減され、計算量が大きく減少する。また、主成分ベクトルを調べることで、データ全体の性質を説明するようなデータの特徴を確認することができる。3.2　K–means 法K–means 法（例えば、参考文献⑸）は、データサンプル間の距離に基づき、入力データを事前に決められた数のグループ（クラスタ）に自動的に分類する手法である。サンプル𝒙𝒙𝒙𝒙𝑖𝑖𝑖𝑖 と、𝒙𝒙𝒙𝒙𝑖𝑖𝑖𝑖 が属するクラスタ𝐶𝐶𝐶𝐶𝑘𝑘𝑘𝑘 （𝑘𝑘𝑘𝑘 =1,2,…,𝐾𝐾𝐾𝐾 ）の重心𝝁𝝁𝝁𝝁𝑘𝑘𝑘𝑘 との距離の二乗の総和𝐾 𝐾 𝐾 𝐾 ��‖𝒙𝒙𝒙𝒙𝑖𝑖𝑖𝑖−𝝁𝝁𝝁𝝁𝑘𝑘𝑘𝑘‖2 𝑘 𝑘 𝑘 𝑘=1 𝒙 𝒙 𝒙 𝒙𝑖𝑖𝑖𝑖∈𝐶𝐶𝐶𝐶𝑘𝑘𝑘𝑘 ⑶を最小化するように各サンプルが所属するクラスタを繰り返し更新し、クラスタ𝐶𝐶𝐶𝐶𝑘𝑘𝑘𝑘 （𝑘𝑘𝑘𝑘 =1,2,…,𝐾𝐾𝐾𝐾 ）を最適化する。クラスタの数𝐾𝐾𝐾𝐾 は、クラスタ内のデータのばらつきが小さいこと及びクラスタ間の距離が離れていることを基準にして決定する。4．地震シナリオの分類面的に類似した地震動分布を持つ地震シナリオ同士を同一のグループに分類する手法について、手法の解析フローと適用結果及び結果に対する考察を記述する。2 MSS技報・Vol.30図２　地震シナリオの分類の解析フロー4.1　地震シナリオの分類手法地震シナリオを分類することを目的として、主成分分析とK–means法を組み合わせた手法を開発した。主成分スコアを入力としたK–means法を行うことで、高次元なデータである地震シナリオを低次元空間において分類することが可能となる。主成分分析を組み合わせることは結果の可視化においても有効である。地震シナリオ等、面的な広がりを持つ高次元のデータは分類結果やデータ点同士の関係性を可視化することに困難が伴うが、低次元の主成分スコアであれば分類されたクラスタ内のデータ点を一覧で表示し、それぞれの特徴を調べることも容易である。地震シナリオに対する分類の解析フローを図２に、処理の手順とその説明を以下に示す。(1)　(2)　長周期地震動シミュレーションにより、𝐷𝐷𝐷𝐷 個の評価地点で計算された最大速度値（cm/s）からなる𝐷𝐷𝐷𝐷 次元実数値ベクトルをひとつのサンプルとするデータを入力とする。入力データのサンプル数はシナリオ数𝑁𝑁𝑁𝑁 となる。𝑁 𝑁 𝑁 𝑁 個のサンプルのそれぞれに対して全評価地点での平均値が０、分散が１となるように線形変換を施す。このような変換をデータの標準化と呼ぶ。標準化を行うことにより、振幅の大きさにのみ依存することなく、地震動の空間的な分布の特徴を捉えた分析が可能となる。(3)　(4)　標準化された分布データに対して主成分分析を行い、主成分ベクトルと主成分スコアを得る。主成分の次元数は累積寄与率の値から決定する。主成分スコアをK–means法によって𝐾𝐾𝐾𝐾 個のクラスタに分類する。以上の手順により、面的に類似した地震動分布を持つ地震シナリオ同士を同一のグループに分類する。4.2　南海トラフシミュレーションデータへの適用南海トラフの369シナリオの地震動シミュレーションデータを使用して、地震シナリオの分類を行った。主成分の次元数𝑃𝑃𝑃𝑃 は、累積寄与率が0.8を越える次元とし、𝑃𝑃𝑃𝑃 =9と定まった。この結果、𝐷𝐷𝐷𝐷 =77,609次元のデータが𝑃𝑃𝑃𝑃 =9次元の主成分スコアとして分析可能となった。主成分ベクトルの各要素を地図上にプロットした結果を図３に示す。各主成分ベクトルはノルム１に正規化されている。𝑝𝑝𝑝𝑝 =1,2の主成分ベクトルは評価地点全体の大域的な傾向を表す分布となっているのに対し、高次の主成分ベクトルは空間方向に高周波な成分の特徴を表現していることがわかる。例えば 𝑝𝑝𝑝𝑝 =1の主成分ベクトル𝒖𝒖𝒖𝒖1 からは、評価範囲の西側で最大速度値が大きくなっている場合に東側では最大速度値が小さくなる傾向があることが読み取れる。図３　主成分ベクトルの可視化-0.02 0.00 0.02 3 MSS技報・Vol.30主成分スコア主成分次元図４　地震シナリオの分類の結果クラスタ数を𝐾𝐾𝐾𝐾 =30として主成分スコアによる地震シナリオの分類を実施し、クラスタごとに主成分スコアをプロットした結果を図４に示す。各パネル内の𝑘𝑘𝑘𝑘 はクラスタ番号を、𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑒𝑒𝑒𝑒 はクラスタに含まれる地震シナリオ数を示している。クラスタ番号は第１主成分スコアのクラスタ内平均値の降順から決定した。主成分スコアは平均値が０となるように変換してプロットしている。主成分スコアの分布が似通っている地震シナリオで各クラスタが構成され、また異なるクラスタ間では主成分スコアの特徴が異なっていることがわかる。𝐾𝐾𝐾𝐾 =30よりクラスタ数が少ない場合では、クラスタ内の主成分スコアのばらつきが大きくなる傾向が見られた。代表シナリオ最大速度値分布=1 =30クラスタ内主成分スコア4.3　考察各クラスタに分類された地震シナリオの主成分スコアとシナリオのパラメータの関係について考察する。分類された地震シナリオの特徴を調べるため、クラスタ内の代表地震シナリオの最大速度値分布と主成分スコア及びクラスタに分類された地震シナリオに設定された震源域・破壊開始点パラメータの頻度分布の一例を図５、図６に示す。なお、クラスタ内の代表シナリオはランダムに選別した。クラスタ𝑘𝑘𝑘𝑘 =1（図５、１段目）とクラスタ𝑘𝑘𝑘𝑘 =30（図５、２段目）は、クラスタ内の第１主成分スコア平均値が最も大きいクラスタと最も小さいクラスタである。クラスタ内の代表シナリオの最大速度値分布においても、最大振幅が出ている地域がそれぞれパラメータ頻度分布震源域小領域パラメータ頻度分布破壊開始点0.0 2.5 5.0 12.5 25.0 50.0 100.0 200.0 （cm/s）図５　クラスタの代表地震シナリオ最大速度値分布と主成分スコア及びシナリオパラメータの頻度分布（𝒌𝒌𝒌𝒌=𝟏𝟏𝟏𝟏,𝟑𝟑𝟑𝟑𝟑𝟑𝟑𝟑 =1,30）4 MSS技報・Vol.30代表シナリオ最大速度値分布=12 =14 0.0 2.5 5.0 12.5 25.0 50.0 100.0 200.0 （cm/s）クラスタ内主成分スコアパラメータ頻度分布震源域小領域パラメータ頻度分布破壊開始点図６　クラスタの代表地震シナリオ最大速度値分布と主成分スコア及びシナリオパラメータの頻度分布（𝒌𝒌𝒌𝒌=𝟏𝟏𝟏𝟏,𝟑𝟑𝟑𝟑𝟑𝟑𝟑𝟑 =12,14）主成分ベクトル𝒖𝒖𝒖𝒖1 の大小に対応していることがわかる。クラスタ内の震源域小領域パラメータ頻度分布に着目すると、クラスタ𝑘𝑘𝑘𝑘 =1は南海トラフ震源域の西側に位置する小領域７、８、９からなるシナリオのみであるのに対し、クラスタ𝑘𝑘𝑘𝑘 =30は南海トラフ震源域の東側に位置する小領域10、11、12からなるシナリオのみで構成されていることがわかる。これらのシナリオでは震源域の位置が最大速度分布に大きく寄与していることがわかる。クラスタ𝑘𝑘𝑘𝑘 =12（図６、１段目）とクラスタ𝑘𝑘𝑘𝑘 =14（図６、２段目）は、第１主成分スコアは似通った値となっているが、第２主成分スコアが大きく異なっている。クラスタ内のパラメータ頻度分布について確認する。震源域小領域においては、両クラスタが類似した地震シナリオから構成されていることがわかる。一方で破壊開始点においては、クラスタ𝑘𝑘𝑘𝑘 =12が南海トラフ震源域の西側に位置する破壊開始点１、２のシナリオのみからなるのに対し、クラスタ𝑘𝑘𝑘𝑘 =14は南海トラフ震源域の北部から北東部に位置する破壊開始点６、８、10のシナリオのみからなっている。これらの地震シナリオでは破壊開始点の位置に従い、地震動の指向性の効果により振幅が大きくなる地域が決まっているといえる。以上の例のように、主成分スコアとシナリオパラメータには関係性があり、地震シナリオの分類によって得られたクラスタ情報を基にしてその関係性を抽出できることがわかった。開発手法の今後の展開として、シナリオパラメータと主成分スコアの関係性を定量的に評価することができれば、任意のシナリオパラメータに対応する地震動分布を主成分ベクトルの線形和として空間的に密に推定することが可能となる。5．評価地点の分類多数の地震シナリオを通して似通った地震動が観測される評価地点同士を同一のクラスタに分類する手法の解析フローと適用結果及び結果に対する考察を記述する。5.1　評価地点の分類手法地震シナリオの分類と同様に、主成分分析とK–means法を組み合わせた手法を構築した。評価地点分類の解析フローを図７に示す。処理の手順を以下に示す。(1)　ある評価地点に対して、𝑁𝑁𝑁𝑁 個のシナリオで計算された最大速度値（cm/s）からなる𝑁𝑁𝑁𝑁 次元実数値ベクトル図７　評価地点の分類の解析フロー5 MSS技報・Vol.30(2)　(3)　をひとつのサンプルとみなしたデータを入力とする。評価地点の分類では、サンプル数は評価地点数𝐷𝐷𝐷𝐷 となる。入力データに対して主成分分析を行い、主成分ベクトルと主成分スコアを得る。主成分の次元数𝑃𝑃𝑃𝑃 は累積寄与率の値から決定する。主成分スコアをK–means法によって𝐾𝐾𝐾𝐾 個のクラスタに分類する。以上の手順により多数の地震シナリオを通して似通った地震動が観測される評価地点同士の分類を実現する。5.2　南海トラフシミュレーションデータへの適用地震シナリオの分類と同様に、南海トラフの海溝型地震369シナリオの地震動シミュレーション結果を使用した。評価地点の分類においては、入力データのサンプル数は𝐷 𝐷 𝐷 𝐷 =77,609、各サンプルの次元数は𝑁𝑁𝑁𝑁 =369である。主成分分析の次元数𝑃𝑃𝑃𝑃 は累積寄与率が0.8を越える次元とし、𝑃𝑃𝑃𝑃 =3と定まった。クラスタ数は𝐾𝐾𝐾𝐾 =10とした。評価地点の所属クラスタを地図上にプロットした結果を図８に示す。同一クラスタに分類された評価地点を同じ色で塗り分けている。富山湾5.3　考察東毛地域別府湾図８　評価地点の分類の結果図９　速度構造モデルの速度層下面深度分布（Vs=1500m/s下面深さ）⑹図８から、評価地点クラスタはおおむね震源域からの位置関係に基づき、空間的に連続した地点から形成されていることがわかる。一方で、群馬県東毛地域や富山湾と別府湾の沿岸部等では、太平洋沿岸地域のクラスタと同じクラスタに分類されている特徴的な評価地点の分布が確認できる。評価地点の分類結果に対し、地震動シミュレーションの計算設定である速度構造モデルの下面深度分布（Vs=1500m/s下面深さ、図９）⑹と比較をとると、特徴的な評価地点が分布している地域で深度が深くなっていることが確認できる。これらの地域では速度構造モデルに従い、各地震シナリオにおいて震源域との位置関係のみに依らず振幅が大きくなるため、南海トラフ震源域に近い評価地点と同じクラスタに分類されたと考えられる。多数の地震シナリオで似通った地震動となる評価地点に自動分類を適用し、得られた評価地点クラスタが震源域からの位置関係や面的な計算設定である速度構造モデルに基づいて形成されていることを確認した。開発した手法の応用への展開として、評価地点クラスタの中で代表地点を定めてクラスタ全体を代表地点と同一視することで、少数の地点での地震動指標値を回帰により推定する手法を面的な地震動指標値分布の推定に発展させることができると考えられる。また、評価地点クラスタとシナリオパラメータとの関係性を抽出する手法⑺を、本稿の開発手法で得られた評価地点クラスタに対しても適用することで、評価地点クラスタを形成する要因をより詳細に分析できる。6．むすび広範囲で面的に計算された地震動シミュレーションデータに対して、地震シナリオ及び評価地点をそれぞれ分類する手法を開発し、南海トラフの海溝型地震を想定した多数の長周期地震動シミュレーション結果に対して適用した。シナリオパラメータや地下構造モデルと分類されたクラスタとの関係性について分析し、得られた結果を地震動分布の推定手法の高度化に適用できる可能性が示唆された。今後は防災・減災に資することを目的とし、地震動の曝露人口や建物被害等のリスク評価値を指標として地震シナリオや評価地点の分析を進めていくことが重要な課題となる。地震動シミュレーションの計算設定パラメータ及び計算結果のデータを利用させていただき、解析手法等についてご指導・ご助言いただいた防災科学技術研究所の関係者様に感謝いたします。本稿に掲載した地図の作成には、国土地理院地図（http://cyberjapandata.gsi.go.jp）6 MSS技報・Vol.30を使用しました。本稿に掲載した図の一部は、GMT⑻を使用して作成しました。参考文献(1) Maeda，T.，Iwaki，A.，Morikawa，N.，Aoi，S.，Fujiwara，H.：Seismic–Hazard Analysis of LongPeriod Ground Motion of Megathrust Earthquakes in the Nankai Trough Based on 3D FiniteDifference Simulation，Seismological Research Letters，87，No.6，1265 ～ 1273（2016）https://doi.org/10.1785/0220160093 (2) Maeda，T.，Fujiwara，H.，Hayakawa，T.，Shimono，S.，Akagi，S.：Cluster Analysis of Long–Period Ground–Motion Simulation Data with Application to Nankai Trough Megathrust Earthquake Scenarios，Journal of Disaster Research，13，No.2，254 ～ 261（2018）https://www.fujipress.jp/jdr/dr/dsstr001300020254/ (3) 青井 真，早川 俊彦，藤原 広行：地震動シミュレータ：GMS，物理探査，57，651～666（2004）(4) Hotelling，H.：Analysis of a complex of statistical variables into principal components，Journal of Educational Psychology，24，No.6，417 ～ 441（1933）(5) MacQueen，J. B.：Some Methods for Classification and Analysis of Multivariate Observations，Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability，1，281 ～297，University of California Press（1967）(6) 防災科学技術研究所：J–SHIS 地震ハザードステーション（2019）https://doi.org/10.17598/nied.0010 (7) Maeda，T.，Fujiwara，H.：Seismic Hazard Visualization from Big Simulation Data: Cluster Analysis of Long–Period Ground–Motion Simulation Data，Journal of Disaster Research，12，No.2，233～240（2017）https://www.fujipress.jp/jdr/dr/dsstr001200020233/ (8) Wessel，P.，Smith，W. H. F.：New version of the Generic Mapping Tools released，Eos，Transactions，American Geophysical Union，76，No.33，329（1995）執筆者紹介赤木 翔2015 年入社。つくば事業部第四技術部所属。地震・津波防災分野の解析に従事。早川 俊彦1998 年入社。つくば事業部第四技術部所属、博士（理学）。地震・津波防災分野の解析・システム開発に従事。下野 五月2005 年入社。つくば事業部第四技術部所属、技術士（応用理学部門）。主として鉄道事業者を対象とした地震防災分野に携わる。