カルマンフィルタによるソフトウェア開発時誤り予測の数値シミュレーション

1 MSS 技報・Vol.30
カルマンフィルタによるソフトウェア開発時誤り予測の数値シミュレーション
Kalman Filtering for Error Prediction in Software Development: Numerical Simulations
矢田部 学＊　岡野 麻子＊＊Manabu Yatabe, Asako Okano
カルマンフィルタ処理は、状態推移を記述する方程式に基づいて現フェーズから次フェーズにおける状態の予測と次フェーズにおける測定結果を反映した予測の修正を交互に行うアルゴリズムである。ソフトウェア開発時の誤りを予測するカルマンフィルタを試作した。それを擬似データに適用し数値シミュレーションを行った。本稿は試作したカルマンフィルタとそのシミュレーション結果について紹介する。
Kalman filtering is an algorithm based on two processes; one predicts next-phase states from thepresent ones using state equations and the other corrects the predicted states with reference tomeasurements at the next phase. We designed a Kalman filter experimentally and applied it to predictingerrors in software development. Numerical simulations of the Kalman filter were carried outusing pseudo data. This report mentions the Kalman filter and its simulations.
＊鎌倉事業部 生産技術部（理博）　＊＊同事業部 同部
1．まえがき
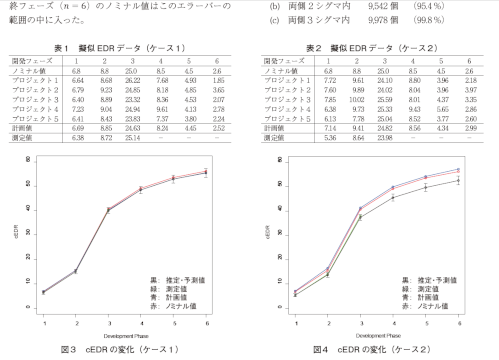
ソフトウェア開発における品質分析・予測に使用されるメトリクスの一つとして、一般的に誤り数が用いられる。我々は、誤り数を誤り検出率という尺度に変換し、プロジェクトの開発期間内で測定される誤り検出率の累積値による予測を行っている。その際、ゴンペルツ曲線を予測モデルとして利用している⑴。ソフトウェア開発の誤り予測においてゴンペルツ曲線が採用されるのは、ウォーターフォール開発における誤り検出率の累積傾向と形状が似ているという理由による⑵。しかし、ゴンペルツ曲線のパラメータは、モデル式を線形化した後で最小二乗法により決定されるため、元のモデル式による予測値の誤差を統計学的に評価しにくいという問題がある。また、ゴンペルツ曲線による予測モデルは測定データのみに基づき、誤りを支配する法則は考慮していない。そこで、それを記述する方程式（状態方程式）があるという仮説を立てた。状態方程式を考慮した予測モデルとしてカルマンフィルタがある。それは、測定を記述する観測方程式の他に状態推移を記述する状態方程式に基づいて、状態量の予測・推定と誤差共分散を評価する計算アルゴリズムであり、航空宇宙分野において実績がある⑶ ⑷。本稿では、ソフトウェア開発時の誤りを記述する状態方程式と観測方程式に基づくカルマンフィルタによる誤り予測手法を提案する⑸。統計学的な議論のためには多数の類似プロジェクトのデータが必要である。現実には、組織や開発チームの変更などにより、類似プロジェクトのデータを多数用意することが困難である。そのため、擬似データを用いて試作したカルマンフィルタの数値シミュレーションを行った。2．仮説と試み2.1　仮説次の仮説を立てた。(a)　ソフトウェア開発において、開発規模・処理対象・作業者などが類似したプロジェクトでの誤り検出率は同じ統計学的な特性を持つ（同じ母集団の標本）。(b)　各開発フェーズにおける誤り検出率を記述できる方程式が存在する。2.2　試み以下のように各開発フェーズにおける誤り検出率を推定・予測するカルマンフィルタの試作と数値シミュレー2 MSS 技報・Vol.30ションを試みた。(a)　プロジェクト計画時にゴールとして設定した誤り検出率（計画値）に基づき、それを記述する方程式を定式化する。(b)　これを状態方程式とし、誤り検出率を推定・予測するカルマンフィルタを設計する。(c)　ソフトウェア開発の誤り検出率の擬似データを作成し、各開発フェーズにおける誤り検出率を推定・予測するカルマンフィルタモデルの数値シミュレーションを行う。3．誤り予測モデル3.1　前提開発フェーズにおける誤り検出率（error detectionrate：以下EDR）の計画値が与えられている。この計画値に基づいてEDR の変化を記述する状態方程式をモデル化する。EDR の測定過程は観測方程式でモデル化する。3.2　状態方程式開発フェーズを𝑛𝑛𝑛𝑛 で表記する。そこでの状態量𝑥𝑥𝑥𝑥𝑛𝑛𝑛𝑛 はEDR だけからなるスカラー量とする。この状態量の推移を記述する状態方程式⑹について述べる。これは過去の類似プロジェクトから得られたEDR の計画値𝑝𝑝𝑝𝑝𝑛𝑛𝑛𝑛 に基づく。計画値の比率 𝑎𝑎𝑎𝑎𝑛𝑛𝑛𝑛−1 ≡ 𝑝𝑝𝑝𝑝𝑛𝑛𝑛𝑛⁄𝑝𝑝𝑝𝑝𝑛𝑛𝑛𝑛−1 は、フェーズ𝑛𝑛𝑛𝑛 − 1 から𝑛𝑛𝑛𝑛 へのEDR の類似プロジェクト固有の変化率を表していると考えられる；フェーズ𝑛𝑛𝑛𝑛 におけるEDRは前フェーズの状態量𝑥𝑥𝑥𝑥𝑛𝑛𝑛𝑛−1 の𝑎𝑎𝑎𝑎𝑛𝑛𝑛𝑛−1 倍とする。状態量は確定的な要素だけでは決まらない。開発環境の背景からの確率的な影響（作りこみ誤りなど）を考える必要がある。そこで、状態方程式にはシステムノイズ𝑢𝑢𝑢𝑢𝑛𝑛𝑛𝑛−1 を考慮する。このノイズは正規分布𝑁𝑁𝑁𝑁􀵫0, 𝜎𝜎𝜎𝜎sys2 􀵯 に従うとする。以上より、状態方程式を以下のように表す：𝑥𝑥𝑥𝑥𝑛𝑛𝑛𝑛 = 𝑎𝑎𝑎𝑎𝑛𝑛𝑛𝑛−1𝑥𝑥𝑥𝑥𝑛𝑛𝑛𝑛−1 + 𝑢𝑢𝑢𝑢𝑛𝑛𝑛𝑛−1 . ⑴3.3　観測方程式測定の状況を表す数学モデルが観測方程式⑹である。開発フェーズ𝑛𝑛𝑛𝑛 におけるEDR が直接測定されるとする。観測方程式には測定環境の確率的な要素（レビュー・テストの観点もれなど）を測定ノイズ𝑣𝑣𝑣𝑣𝑛𝑛𝑛𝑛 として考慮する。このノイズは正規分布𝑁𝑁𝑁𝑁(0, 𝜎𝜎𝜎𝜎obs2 ) に 従うとする。以上より、EDR の測定値𝑦𝑦𝑦𝑦𝑛𝑛𝑛𝑛 に関する観測方程式を以下のように表す：𝑦𝑦𝑦𝑦𝑛𝑛𝑛𝑛 = 𝑥𝑥𝑥𝑥𝑛𝑛𝑛𝑛 + 𝑣𝑣𝑣𝑣𝑛𝑛𝑛𝑛 . ⑵3.4　カルマンフィルタ状態方程式⑴と観測方程式⑵で表される処理系にカルマンフィルタ⑹を適用する。図１において、「システム」は状態方程式、「測定」は観測方程式の処理に対応し、測定の結果が「カルマンフィルタ」に入力される。カルマンフィルタは状態量に対して、状態方程式に基づく予測（時間更新）と測定に基づく推定（観測更新）を交互に行うアルゴリズムである。このため、更新を表す２種類の記号を必要とする。状態の予測に関する更新を、開発フェーズを指定する“ 𝑛𝑛𝑛𝑛 ” で記述する。測定に関する更新を“(±) ” で記述する。ここで“(+) ” は測定後、“(−) ” は測定前の状態を表す。以下に時間更新と観測更新の処理をまとめる。なお、推定量であることを明示するために状態量にはハット“ 􀷡 ” をつけて表す。3.4.1　時間更新現フェーズ𝑛𝑛𝑛𝑛 から次フェーズ𝑛𝑛𝑛𝑛 + 1 の状態量（EDR）を予測する。状態量𝑥𝑥𝑥𝑥𝑛𝑛𝑛𝑛 とその誤差共分散（＊1 𝑃𝑃𝑃𝑃𝑛𝑛𝑛𝑛 に関して次の処理を行う⑹。(a)　状態量（予測） 𝑥𝑥𝑥𝑥􀷜𝑛𝑛𝑛𝑛+1(−) = 𝑎𝑎𝑎𝑎𝑛𝑛𝑛𝑛𝑥𝑥𝑥𝑥􀷜𝑛𝑛𝑛𝑛(+)(b)　誤差共分散（予測） 𝑃𝑃𝑃𝑃𝑛𝑛𝑛𝑛+1(−) = 𝑎𝑎𝑎𝑎𝑛𝑛𝑛𝑛 2 𝑃𝑃𝑃𝑃𝑛𝑛𝑛𝑛(+) + 𝑄𝑄𝑄𝑄𝑛𝑛𝑛𝑛ここで、誤差共分散の中の𝑄𝑄𝑄𝑄𝑛𝑛𝑛𝑛 はシステムノイズ共分散（＊1と呼ばれるもので、式⑴のシステムノイズが従う𝐾𝐾𝐾𝐾𝑛𝑛𝑛𝑛遅延遅延𝑣𝑣𝑣𝑣𝑛𝑛𝑛𝑛𝑦𝑦𝑦𝑦𝑛𝑛𝑛𝑛𝑢𝑢𝑢𝑢𝑛𝑛𝑛𝑛−1+++++ − ++𝑥𝑥𝑥𝑥􀷜𝑛𝑛𝑛𝑛(+)𝑥𝑥𝑥𝑥􀷜𝑛𝑛𝑛𝑛−1(+)𝑥𝑥𝑥𝑥􀷜𝑛𝑛𝑛𝑛(−)𝑥𝑥𝑥𝑥𝑛𝑛𝑛𝑛 = 𝑎𝑎𝑎𝑎𝑛𝑛𝑛𝑛−1𝑥𝑥𝑥𝑥𝑛𝑛𝑛𝑛−1 + 𝑢𝑢𝑢𝑢𝑛𝑛𝑛𝑛−1𝑥𝑥𝑥𝑥𝑛𝑛𝑛𝑛𝑦𝑦𝑦𝑦𝑛𝑛𝑛𝑛 = 𝑥𝑥𝑥𝑥𝑛𝑛𝑛𝑛 + 𝑣𝑣𝑣𝑣𝑛𝑛𝑛𝑛𝑥𝑥𝑥𝑥􀷜𝑛𝑛𝑛𝑛 − = 𝑎𝑎𝑎𝑎𝑛𝑛𝑛𝑛−1𝑥𝑥𝑥𝑥􀷜𝑛𝑛𝑛𝑛−1(+)𝑥𝑥𝑥𝑥􀷜𝑛𝑛𝑛𝑛 + = 𝑥𝑥𝑥𝑥􀷜𝑛𝑛𝑛𝑛 − + 𝐾𝐾𝐾𝐾𝑛𝑛𝑛𝑛 𝑦𝑦𝑦𝑦𝑛𝑛𝑛𝑛 − 𝑥𝑥𝑥𝑥􀷜𝑛𝑛𝑛𝑛 −システム 測定 カルマンフィルタ𝑎𝑎𝑎𝑎𝑛𝑛𝑛𝑛−1 𝑎𝑎𝑎𝑎𝑛𝑛𝑛𝑛−1𝑥𝑥𝑥𝑥𝑛𝑛𝑛𝑛−1図1　カルマンフィルタの処理3 MSS 技報・Vol.30正規分布の分散と𝑄𝑄𝑄𝑄𝑛𝑛𝑛𝑛 = 𝜎𝜎𝜎𝜎sys2 の関係がある。この処理では、状態方程式⑴に基づいて、開発フェーズ𝑛𝑛𝑛𝑛 における状態量𝑥𝑥𝑥𝑥􀷜𝑛𝑛𝑛𝑛(+) から次フェーズの状態量𝑥𝑥𝑥𝑥􀷜𝑛𝑛𝑛𝑛+1(−) を予測する。現フェーズの誤差共分散𝑃𝑃𝑃𝑃𝑛𝑛𝑛𝑛(+) にシステムノイズ共分散𝑄𝑄𝑄𝑄𝑛𝑛𝑛𝑛 を考慮して、次のフェーズの誤差共分散𝑃𝑃𝑃𝑃𝑛𝑛𝑛𝑛+1(−)を予測する。3.4.2　観測更新測定結果に基づいて状態量（EDR）の補正を行い状態量の真値を推定する。状態量とその誤差共分散に関して次の処理を行う⑹。(a)　カルマンゲイン 𝐾𝐾𝐾𝐾𝑛𝑛𝑛𝑛 = 𝑃𝑃𝑃𝑃𝑛𝑛𝑛𝑛(−)⁄[𝑃𝑃𝑃𝑃𝑛𝑛𝑛𝑛(−) + 𝑅𝑅𝑅𝑅𝑛𝑛𝑛𝑛](b)　状態量（推定） 𝑥𝑥𝑥𝑥􀷜𝑛𝑛𝑛𝑛(+) = 𝑥𝑥𝑥𝑥􀷜𝑛𝑛𝑛𝑛(−) + 𝐾𝐾𝐾𝐾𝑛𝑛𝑛𝑛[𝑦𝑦𝑦𝑦𝑛𝑛𝑛𝑛 − 𝑥𝑥𝑥𝑥􀷜𝑛𝑛𝑛𝑛(−)](c)　誤差共分散（推定） 𝑃𝑃𝑃𝑃𝑛𝑛𝑛𝑛(+) = (1 − 𝐾𝐾𝐾𝐾𝑛𝑛𝑛𝑛)𝑃𝑃𝑃𝑃𝑛𝑛𝑛𝑛(−)ここで、カルマンゲインの中に現れている𝑅𝑅𝑅𝑅𝑛𝑛𝑛𝑛 は測定ノイズ共分散（＊1と呼ばれるもので、式⑵の測定ノイズが従う正規分布の分散と𝑅𝑅𝑅𝑅𝑛𝑛𝑛𝑛 = 𝜎𝜎𝜎𝜎obs2 の関係がある。測定前の誤差共分散と測定ノイズ共分散からカルマンゲインが決まる。このゲインを測定値と予測値の差分𝑦𝑦𝑦𝑦𝑛𝑛𝑛𝑛 − 𝑥𝑥𝑥𝑥􀷜𝑛𝑛𝑛𝑛(−) に乗じた量で予測値を修正して、測定を反映した推定値𝑥𝑥𝑥𝑥􀷜𝑛𝑛𝑛𝑛(+) が得られる。測定後の誤差共分散𝑃𝑃𝑃𝑃𝑛𝑛𝑛𝑛(+) は、(1 − 𝐾𝐾𝐾𝐾𝑛𝑛𝑛𝑛) < 1 が成り立つので、測定前𝑃𝑃𝑃𝑃𝑛𝑛𝑛𝑛(−) より小さくなる。3.5　累積誤り検出率とその誤差EDR の推定値𝑥𝑥𝑥𝑥􀷜𝑘𝑘𝑘𝑘(+) （𝑘𝑘𝑘𝑘 = 1,2, ⋯ ）を累積して、開発フェーズ𝑛𝑛𝑛𝑛 における累積誤り検出率（cumulative errordetection rate：以下cEDR）を算出する：𝑐𝑐𝑐𝑐𝑛𝑛𝑛𝑛 = [𝑥𝑥𝑥𝑥􀷜1(+) + 𝑥𝑥𝑥𝑥􀷜2(+) + ⋯+ 𝑥𝑥𝑥𝑥􀷜𝑛𝑛𝑛𝑛−1(+)] + 𝑥𝑥𝑥𝑥􀷜𝑛𝑛𝑛𝑛(+)= 𝑐𝑐𝑐𝑐𝑛𝑛𝑛𝑛−1 + 𝑥𝑥𝑥𝑥􀷜𝑛𝑛𝑛𝑛(+) . ⑶カルマンフィルタが出力する誤差共分散𝑃𝑃𝑃𝑃𝑛𝑛𝑛𝑛(+) はEDR の推定値𝑥𝑥𝑥𝑥􀷜𝑛𝑛𝑛𝑛(+) の分散を意味する。これより、開発フェーズ𝑛𝑛𝑛𝑛 におけるEDR 推定値の誤差を表す標準偏差は𝜎𝜎𝜎𝜎𝑥𝑥𝑥𝑥𝑛𝑛𝑛𝑛 = 􀶥𝑃𝑃𝑃𝑃𝑛𝑛𝑛𝑛(+) である。これに基づいてcEDR の標準偏差を算出する。各開発フェーズにおけるEDR の測定は独立であると仮定する。誤差伝播則⑺をcEDR の定義式⑶に適用すると、フェーズ𝑛𝑛𝑛𝑛 におけるcEDR の標準偏差は以下のように表現できる：𝜎𝜎𝜎𝜎𝑐𝑐𝑐𝑐𝑛𝑛𝑛𝑛 = 􀶧𝜎𝜎𝜎𝜎𝑥𝑥𝑥𝑥12 + 𝜎𝜎𝜎𝜎𝑥𝑥𝑥𝑥22 + ⋯+ 𝜎𝜎𝜎𝜎𝑥𝑥𝑥𝑥𝑛𝑛𝑛𝑛2 . ⑷4．数値シミュレーション擬似データを用いて、前章で述べた誤り予測のシミュレーションを行った。EDR の測定は、類似プロジェクトの母集団からそれに属するプロジェクトの標本を抽出することに相当する。この母集団は正規分布𝑁𝑁𝑁𝑁(𝜇𝜇𝜇𝜇, 𝜎𝜎𝜎𝜎2) に従うとする。図２に母集団に属する一つのプロジェクトに着目したときのEDR 測定の概念を示す。このプロジェクトの開発フェーズ𝑘𝑘𝑘𝑘 におけるEDR は真値𝜇𝜇𝜇𝜇𝑘𝑘𝑘𝑘 を中心として標準偏差𝜎𝜎𝜎𝜎 で広がっている。このため、一つの開発フェーズ𝑘𝑘𝑘𝑘 に着目しても、複数回測定を行うと測定するたびに標本値が異なる。ここでの分散𝜎𝜎𝜎𝜎2 は状態方程式⑴の中にあるシステムノイズが従う正規分布の分散と同一とする（𝜎𝜎𝜎𝜎 ≡ 𝜎𝜎𝜎𝜎sys ）。4.1　プロジェクトの擬似データ以下の手順でEDR の擬似データを作成する。擬似データのノミナル値（現実のソフトウェア開発では真値）はソフトウェア開発関連の書籍⑵ ⑻を参考にした。4.1.1　擬似データ作成手順(a)　EDR のノミナル値𝜇𝜇𝜇𝜇𝑛𝑛𝑛𝑛 （𝑛𝑛𝑛𝑛 = 1,2, ⋯ ,6 ）を与える。各𝑛𝑛𝑛𝑛 は実際の開発フェーズ（設計やテストなど）に相当する。(b)　⒜で与えた𝜇𝜇𝜇𝜇𝑛𝑛𝑛𝑛 のまわりに正規分布𝑁𝑁𝑁𝑁(𝜇𝜇𝜇𝜇𝑛𝑛𝑛𝑛, 𝜎𝜎𝜎𝜎2) に従う擬似乱数を発生させて擬似プロジェクトのデータを作成する（過去のプロジェクトの模擬）。(c)　⒝のデータセットの平均をとり、新たなプロジェクトの計画値とする。(d)　新たなプロジェクトのEDR 測定を模擬するデータは、⒝と同様に𝑁𝑁𝑁𝑁(𝜇𝜇𝜇𝜇𝑛𝑛𝑛𝑛, 𝜎𝜎𝜎𝜎2) に従う擬似乱数を発生させて作成する。真値測定値開発フェーズEDR𝑘𝑘𝑘𝑘𝑥𝑥𝑥𝑥𝑘𝑘𝑘𝑘 𝑁𝑁𝑁𝑁(𝜇𝜇𝜇𝜇𝑘𝑘𝑘𝑘, 𝜎𝜎𝜎𝜎2)母集団{𝑥𝑥𝑥𝑥1, 𝑥𝑥𝑥𝑥2, ⋯ , 𝑥𝑥𝑥𝑥𝑘𝑘𝑘𝑘, ⋯ }𝜇𝜇𝜇𝜇𝑘𝑘𝑘𝑘標本抽出1 2 ⋯ ⋯あるプロジェクトのEDR図2　EDR の測定4 MSS 技報・Vol.304.2　シミュレーション結果4.1節に述べた手順でEDRを模擬する擬似データを生成しcEDR を評価するシミュレーションを行った。代表的な例として、推定・予測値のエラーバー内にノミナル値が入るケース１と入らないケース２を以下に示す。さらに、これらの結果を踏まえてケース３では、多数のデータに対して推定・予測値のエラーバー内にノミナル値が含まれる割合を調べる。4.2.1　ケース１表１のデータを用いてcEDR の変化を算出した。過去の類似プロジェクトの数は５とした。また、EDR の測定は𝑛𝑛𝑛𝑛 = 3 までとした。つまり、𝑛𝑛𝑛𝑛 = 3 までは時間更新（予測）と観測更新（推定）を行うが、𝑛𝑛𝑛𝑛 = 4 以降の測定は行わず、予測値𝑥𝑥𝑥𝑥􀷜𝑛𝑛𝑛𝑛(−) を推定値𝑥𝑥𝑥𝑥􀷜𝑛𝑛𝑛𝑛(+) とした。状態量の初期値は計画値で代用し、誤差共分散の初期値は𝑃𝑃𝑃𝑃0(−) = 10 とした。また、システムノイズと測定ノイズの標準偏差は、それぞれ𝜎𝜎𝜎𝜎sys = 0.7 及び𝜎𝜎𝜎𝜎obs = 0.7 とした。そのときのcEDR の変化を図３に示す。ここで示した推定・予測値のエラーバーは式⑷から算出した。ここでは、推定値の両側に１シグマをとっている。最終フェーズ（𝑛𝑛𝑛𝑛 = 6 ）のノミナル値はこのエラーバーの範囲の中に入った。4.2.2　ケース２表２のデータを用いて、ケース１と同様のシミュレーションを行った。その結果が図４である。シミュレーションに関する条件はケース１と同様である。最終フェーズのノミナル値は両側１シグマのエラーバー内には入らなかった。この例では両側２シグマのエラーバーを考えるとノミナル値はエラーバー内に入る。4.2.3　ケース３ケース１と２のシミュレーション結果から、推定・予測値のエラーバーとノミナル値の関係はデータにより異なる。そこで、多数の擬似データに対してエラーバー内に入るノミナル値の割合を調べた。擬似データのセットを104 個用意した（生成方法はケース１、２と同様）。各データセットは、開発フェーズ𝑛𝑛𝑛𝑛 = 3 までEDR の測定を行い、𝑛𝑛𝑛𝑛 = 4 以降は測定を行わない条件とした（ケース１、２と同様）。これら104 個のデータセットについて、最終フェーズ𝑛𝑛𝑛𝑛 = 6 におけるEDR の推定・予測値のエラーバー内にノミナル値が入ったデータセットの個数を調べた。その結果を次に示す。(a)　両側１シグマ内 6,856 個 （68.6 %）(b)　両側２シグマ内 9,542 個 （95.4 %）(c)　両側３シグマ内 9,978 個 （99.8 %）表1　擬似EDR データ（ケース１）開発フェーズ1 2 3 4 5 6ノミナル値6.8 8.8 25.0 8.5 4.5 2.6プロジェクト１ 6.64 8.68 26.22 7.68 4.93 1.85プロジェクト２ 6.79 9.23 24.85 8.18 4.85 3.65プロジェクト３ 6.40 8.89 23.32 8.36 4.53 2.07プロジェクト４ 7.23 9.04 24.94 9.61 4.13 2.78プロジェクト５ 6.41 8.43 23.83 7.37 3.80 2.24計画値6.69 8.85 24.63 8.24 4.45 2.52測定値6.38 8.72 25.14 － － －1 2 3 4 5 60 10 20 30 40 50 60Development PhasecEDR黒： 推定・予測値緑： 測定値青： 計画値赤： ノミナル値図3　cEDR の変化（ケース１）表2　擬似EDR データ（ケース２）開発フェーズ1 2 3 4 5 6ノミナル値6.8 8.8 25.0 8.5 4.5 2.6プロジェクト１ 7.72 9.61 24.10 8.80 3.96 2.18プロジェクト２ 7.60 9.89 24.02 8.04 3.96 3.97プロジェクト３ 7.85 10.02 25.59 8.01 4.37 3.35プロジェクト４ 6.38 9.73 25.33 9.43 5.65 2.86プロジェクト５ 6.13 7.78 25.04 8.52 3.77 2.60計画値7.14 9.41 24.82 8.56 4.34 2.99測定値5.36 8.64 23.98 － － －1 2 3 4 5 60 10 20 30 40 50 60Development PhasecEDR黒： 推定・予測値緑： 測定値青： 計画値赤： ノミナル値図4　cEDR の変化（ケース２）5 MSS 技報・Vol.30カルマンフィルタ理論の誤差は正規分布に従うノイズを前提としている。したがって、EDR の推定・予測値𝑥𝑥𝑥𝑥􀷜𝑛𝑛𝑛𝑛 は正規分布に従う確率変数の実現値とみなすことができる。確率変数が正規分布に従うとき、これらの一次結合で定義される新たな確率変数も正規分布に従う⑼（再生性）。その結果、式⑶で算出されるcEDR も正規分布に従う確率変数の実現値になる。理論上、正規分布に従うデータに対しては、平均値の両側1 シグマ内には68.3 %、２シグマ内には95.5 %、３シグマ内には99.7 % のデータが入る⑼。シミュレーション結果を、ノミナル値を中心とした推定・予測値の分布とみなすと、理論値との比較ができる；ノミナル値のまわりに推定・予測値が正規分布に従い広がっている。上の結果はこれを満たしているように見えるが、注意が必要である。これについては4.3 節で議論する。4.3　考察4.2 節のシミュレーション結果の考察をまとめる。4.3.1　ケース１と２の比較ケース１では、最終開発フェーズ（𝑛𝑛𝑛𝑛 = 6 ）において、EDR のノミナル値がエラーバー内（両側１シグマ）に入った。しかし、ケース２ではエラーバー内に入らなかった。ケース１とケース２の違いは以下のように考えられる。カルマンフィルタの初期値（𝑛𝑛𝑛𝑛 = 1 の計画値）とそこでの測定値の差分を見ると、ケース１のほうがケース２より小さい。そのため、ケース１の方がカルマンフィルタによる予測が良くなったと考えられる。ケース２におけるノミナル値と推定・予測値の差異の改善方法として、例えば状態方程式⑴にバイアス項𝑏𝑏𝑏𝑏 を追加して𝑥𝑥𝑥𝑥𝑛𝑛𝑛𝑛 = 𝑎𝑎𝑎𝑎𝑛𝑛𝑛𝑛−1𝑥𝑥𝑥𝑥𝑛𝑛𝑛𝑛−1 + 𝑏𝑏𝑏𝑏𝑛𝑛𝑛𝑛−1 + 𝑢𝑢𝑢𝑢𝑛𝑛𝑛𝑛−1とする方式などが考えられる。ただし、このバイアス項はケース１の結果を含めて決定しなければならず、状態方程式のモデル化が複雑になる。現実のソフトウェア開発では、このバイアス項は計画値の妥当性に関連していると考えられる。適切な状態方程式の表現については今後の検討が必要である。4.3.2　ケース３誤差共分散𝑃𝑃𝑃𝑃𝑛𝑛𝑛𝑛(±) には、状態方程式⑴のシステムノイズと観測方程式⑵の測定ノイズが反映されている。測定が行われると、その結果に基づいて予測値が修正されるため誤差共分散が𝑃𝑃𝑃𝑃𝑛𝑛𝑛𝑛(−) から𝑃𝑃𝑃𝑃𝑛𝑛𝑛𝑛(+) へ減少する。この減少は次フェーズのシステムノイズと測定ノイズに影響を与える。そのため、これらノイズを変更せずに測定条件だけを変更すると、4.2 節で述べた「ノミナル値がエラーバー内に入る割合」が崩れる。一般に、測定の回数を増やすほど、精度が上がりエラーバーは短くなる。これは、ベイズ統計の観点では「事前確率分布から事後確率分布への更新に伴う分散の減少」と解釈できる⑽。例として、測定をする開発フェーズを増やして𝑛𝑛𝑛𝑛 = 4以降も測定する場合を考える。測定はシステムに影響する外乱を制御する行為とみなせるので、システムノイズはケース３のシミュレーションより小さめに設定する必要がある。他方、測定ノイズは、一回の測定ごとに加算されるので、ケース３より大きめに設定する必要がある。測定条件が変更されても、状況に対応したシステムノイズと測定ノイズを再設定すれば、「ノミナル値がエラーバー内に入る割合」は保存される。カルマンフィルタ理論のノイズは正規性を前提としているので、このことを意識することは重要である。今回のシミュレーションでは、システムノイズと測定ノイズは全開発フェーズで一定値を用いた。モデルの精密化のためには、測定の有無を考慮して開発フェーズごとに設定することなどが考えられる。上述のことは、カルマンフィルタのパラメータ設定とも関連している。カルマンフィルタを処理するためには、次に示す４種類のアプリオリなパラメータを設定する必要がある。(a)　初期値に関して ⒤ 状態量：𝑥𝑥𝑥𝑥􀷜0(−)ⅱ 誤差共分散：𝑃𝑃𝑃𝑃0(−)(b)　ノイズに関して ⅲ システムノイズ共分散：𝑄𝑄𝑄𝑄𝑛𝑛𝑛𝑛ⅳ 測定ノイズ共分散：𝑅𝑅𝑅𝑅𝑛𝑛𝑛𝑛適切でないパラメータを設定するとカルマンフィルタは有効に機能しない。これらを設定するための一般的な手段はない。シミュレーション結果に基づいてパラメータの試行錯誤的なチューニングが必要である。その際の手段として、「ノミナル値がエラーバー内に入る割合」を意識することは有用と考えられる。5．むすびEDR を状態量として、これを推定・予測するカルマンフィルタを試作した。この中には、EDR の推移を記述した状態方程式と統計学に基づく誤差の評価（誤差共分散）が考慮されている。その試作ツールを用いて、数値シミュレーションを実施し、ソフトウェア開発時の誤り予測へのカルマンフィルタの利用可能性を示した。今後は、実際のプロジェクトの実績データを使って検証していく予定である。本稿ではEDRのみからなるスカラーの状態量に関するカルマンフィルタについて述べた。カルマンフィルタの6 MSS 技報・Vol.30状態量としては、例えばEDR とcEDR の２成分からなるベクトル量を考えることもできる。出発点となる状態量、状態方程式、観測モデルの決め方は一意ではない。有効なカルマンフィルタを設計するために、これらの検討は重要である。　　　　　　　　　　　　　　　　　　　　　　　　　＊1　本モデルはEDR のみからなる1 成分の状態量を扱っているので、{𝑃𝑃𝑃𝑃𝑛𝑛𝑛𝑛, 𝑄𝑄𝑄𝑄𝑛𝑛𝑛𝑛, 𝑅𝑅𝑅𝑅𝑛𝑛𝑛𝑛} は実際には「…共分散」ではなく「…分散」である。一般にはベクトルと行列で記述されている数式が、本モデルではスカラー量の関係式となっている。参考文献(1) 岡野 麻子，岡田 政之，土屋 義兼：定量的プロジェクト管理におけるソフトウェア品質予測モデルの構築と適用，MSS 技報，26（2016）http://www.mss.co.jp/technology/report/pdf/26_06.pdf(2) 三觜 武：ソフトウェアの品質評価法―統計的管理へのアプローチ，181 ～ 191，日科技連出版社（1981）(3) 西村 敏充：カルマン・フィルタ理論の飛翔体システムへの応用，システムと制御，22，No.1，10 ～ 19（1978）(4) 岩田 隆敬：宇宙分野におけるカルマンフィルタの応用，計測と制御，56，No.9，668 ～ 674（2017）(5) 矢田部 学：擬似データを用いたカルマンフィルタによる不具合予測，Fy18 品証生産性向上セミナーQ-2，社内講座資料（2018）(6) Gelb，A.，ed.：Applied　Optimal　Estimation，107～ 119，MIT Press（1974）(7) Lichten，W.（村上 雅章 訳）：計測データと誤差解析の入門，54 ～ 55，ピアソン・エデュケーション（2004）(8) Jones，C.（鶴保 征城，富野 壽 監訳）：ソフトウェア開発の定量化手法 第２版，394 ～ 399，共立出版（1998）(9) 東京大学教養学部統計学教室 編：統計学入門，122・151，東京大学出版会（1991）(10) 松原 望：入門ベイズ統計―意思決定の理論と発展，17 ～ 19，東京図書（2008）執筆者紹介矢田部 学1986 年入社。つくば事業部で宇宙分野の解析や金融工学に従事。2004 年から鎌倉事業部で宇宙・防衛分野のモデリングや統計解析に従事。博士（理学）。岡野 麻子1997 年入社。入社以来、鎌倉事業部で防衛分野に従事。2005 年から品質保証に従事。2012 年から生産技術部門でプロセス改善に従事。