最小二乗法による温度変化曲線のモデル化と評価

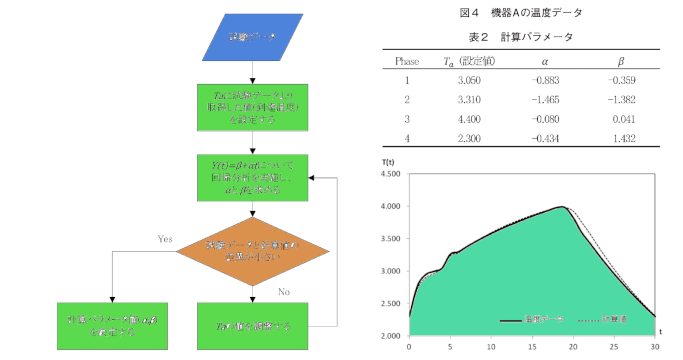
1 MSS技報・Vol.27＊鎌倉事業部　宇宙第一技術部
最小二乗法による温度変化曲線のモデル化と評価
Modeling and evaluation of the temperature change curve by using the method of least squares
橘田 悠＊　Haruka Kitta
　物質の温度は、単純な増加や減少といった直線的な変化だけでなく、一定値に収束するような指数関数的な変化、あるいはこれらを組み合わせた変化をすることが一般的である。そのような温度変化をモデル化する場合、直線的な変化を数式に当てはめることは比較的容易であるが、複雑な曲線的な変化を数式に当てはめることは難しい。本稿では、衛星搭載機器間の熱伝導を取り上げ、曲線的な温度変化のモデル化、最小二乗法によるパラメータの決定方法、およびその評価について示す。
　Material temperature shows linear, exponential or their composite changes in general. It iscomparatively easy to fit the temperature change models to measurement data for the linear trendbut not for complex curvilinear one. This paper mentions a mathematical model for the thermalconductivity between instruments in an artificial satellite. Moreover this paper shows curvilineartemperature changes modeling, parameters estimation using the least-squares method, andestimation errors evaluation.
1．まえがき
　一般的にモデル化とは、対象とする事象を簡略化、抽象化することを指し、多くの分野で用いられる技術の一つである。宇宙分野でも、衛星の軌道や姿勢、熱、電力などの物理現象の変化をモデル化し、数式化することは、これらの現象について数値解析を行う上で重要となる。　本稿では、宇宙空間における衛星機器の温度をターゲットとし、温度変化曲線のモデル化を試みた。直線的な温度変化のモデル化は比較的容易なため本稿では取り上げず、一定値に収束する温度変化をモデル化する点に着目した。まず、温度変化の定式化について述べ、次に、温度変化曲線に当てはめるための計算パラメータ決定法について述べる。最後に、任意の曲線的な温度変化のモデル化を事例として示し、その評価結果を述べる。　アプローチの手順は以下の通りである。⑴　衛星機器の温度変化を数学的に捉えるため、熱伝導のフーリエの法則をもとにモデル式を導出した。⑵　展開した式に基づいて、温度算出のための計算パラメータ値を選定した。⑶　選定した計算パラメータをモデル化対象となる温度変化曲線に当てはめた。計算パラメータ値の決定には、最小二乗法を適用した。⑷　任意の温度データを例に、⑵の手法により決定した計算パラメータ値を(1)の式に当てはめ、温度変化曲線をモデル化した。⑸　モデル評価として、計算パラメータ値の評価を実施した。2．温度変化曲線の当てはめ2.1　熱伝導モデル適用による温度変化の定式化　熱の伝わり方は、伝導、対流、放射の3タイプがあるが、宇宙空間では伝導と放射が支配的である。したがって、衛星の熱解析は伝導と放射のモデルに基づいて行われることが多い。本稿では衛星搭載機器間の熱伝導に着目した。　一般的な温度変化の数学モデルの基本概念を図１に示す。宇宙空間での衛星機器の温度には、外部環境に依存する外界温度や機器の熱容量が影響する。本稿では機器aと機器bという異なる機器を仮定し、他の機器からの熱伝導を考慮したモデルとした。　熱伝導を表すモデルはフーリエの法則（1）：q =－kdT /dx（q：熱流束[Wm-2]、k：熱伝導率[Wm-1K-1]、dT/dx：温度図１　温度変化の数学モデルの基本概念2 MSS技報・Vol.27最小二乗法が挙げられる。最小二乗法とは、適当なモデルから想定される1次関数、対数曲線など特定の関数を用いて近似するときに、想定する関数が測定値に対してよい近似となるように、残差の二乗和を最小とするような計算パラメータを決定する方法である。本稿では、モデル化の対象となる温度データに当てはまるように計算パラメータを決定する方法として適切な手法であると判断し、採用した。　モデル化の対象となる温度データがある場合、2.1節で選定した計算パラメータのうち、Taは到達する温度とみなすことができ、既知の計算パラメータとなる。　ここでTa>T(0) のとき、式⑷において、とおくと、式⑷は式⑸のように変形できる。⑸さらに、とし、式⑹に変形した。⑹　なお、Ta<T(0) のときは、y(t) ≡T(t) －Ta，y0≡T(0) －Taとおく。　以上の式展開により、式⑷の温度変化曲線を線形化することができた。その後は、式⑹に最小二乗法を適用し、αとβを決定すれば、式⑷における計算パラメータである－K/C とT(0) が導かれる。本稿では、MicrosoftExcelの回帰分析ツールを用いて最小二乗法を実施した。勾配[Km-1]）を出発点としており、本稿でもこれを適用する。フーリエの法則より、断面積A [m2]を通過して単位時間に節点j から節点i に流れ込む熱エネルギーQ [W]は式⑴のように示される。⑴　さらに、伝導コンダクタンスK≡kA/Δx [WK-1]とおくと、単位時間あたりに流入する熱エネルギーは式⑵のように簡潔に表現される。⑵　図１にて、機器間に流れ込む熱エネルギーを考えた場合、平衡状態となった時の温度をTa [K]、時刻t における温度をT(t) [K]とおく。式⑵の形の熱エネルギーが温度変化を生じさせるので、熱容量をC [JK-1]として、エネルギーの関係は式⑶のように表すことができる。⑶微分方程式⑶を解くと、となり、さらに指数関数の表現にすると、となり、最終的に時刻tにおける温度は式⑷で示される。⑷　式⑷においてα≡－K/C とし、T(0) 、Ta、α に任意の値を代入した。代入した値を表１に、代入した結果のグラフを図２に示す。　ケース1とケース2より、TaとT(0) の大小関係によって、下降または上昇傾向の収束曲線となることがわかる。また、ケース1とケース3からは、－K/C の大きさが収束曲線の傾きに影響することがわかる。　以上のことから、TaとT(0) 、－K/C の値を計算パラメータとし、これらの値をモデル化の対象となる温度データ（例えば、衛星機器の温度の実測値）に合わせて決定することができれば、温度変化曲線のモデル化に式⑷が適用できると考えた。2.2　最小二乗法による温度変化曲線の当てはめ　2.1節で選定した計算パラメータ値の決定方法として、図２　代入結果(ケース1～ケース3)表１　代入した値一覧3 MSS技報・Vol.27計算パラメータの決定手順を図３に示す。図中の試験データとはモデル化の対象となる温度データ、計算値とは本稿で示す手法によって求められた温度値を指す。　まず、Taに試験データより取得した値を設定する。次に、Y(t) ≡ln y(t) について回帰分析を実施し、α とβ を求める。その後、試験データ曲線と計算値の曲線の差異を判定する。差異が大きい場合は、Taの値を変更し、変更後の値で回帰分析を実施する。以上の手順を試験データと計算値の差異が小さくなるまで繰り返す。2.3　温度変化曲線のモデル化事例　2.2節で述べた計算パラメータ値の決定手法を用い、温度変化曲線をモデル化した事例を挙げる。機器Aの温度データのグラフを図４に示す。　まずは、温度データの傾きによって時刻をいくつかのフェーズに分割し、フェーズごとの温度変化曲線の当てはめを実施した。機器Aは、時刻t =0～19にかけて上昇傾向、時刻t =19～30にかけて下降傾向にある。上昇中の温度傾向をさらに3つに分けることとし、計4つのフェーズに分割した。各フェーズで決定した計算パラメータ値を表２に、機器Aの温度データと計算値の温度変化曲線を重ねたグラフを図５に示す。　表２のTa（設定値）は、図３の「Taの値を調整する」作業により、最終的に決定した値である。初期値は図４から読み取った値を設定するが、フェーズによっては、5～6回Taの値を調整した。　本事例により、曲線的な温度変化が一つのパラメータの設定により決定できることが示された。3．計算パラメータの評価　Microsoft Excelの回帰分析ツールの出力情報には相関係数や標準誤差、分散などが含まれ、回帰直線を評価することができる。これらの出力情報を用いて、2.3節で示した機器Aのモデルの計算パラメータの決定値の評価を実施した。　フェーズ1の回帰分析の結果の抜粋を表３に示す。評価結果から抽出した次の2つの情報を用いてモデルの有意性を評価する。なお、表３に表記されているt は検定に用いるt統計量を意味し、式中で用いた時刻とは異なる。図３　計算パラメータの決定手順概要表２　計算パラメータ図４　機器Aの温度データ図５　温度変化曲線のモデル化事例4 MSS技報・Vol.27⑴　相関係数（R）（＊1）　機器Aの温度データと回帰直線の相関を示す。値が1に近いほど回帰直線が機器Aの温度データと一致していると判断できる。一般的にRが0.60～0.70 以上を示すと相関があると考えられる（2）。表３では、0.998を示しており、高い相関が認められると判断する。⑵　P－値　「回帰方程式のすべての係数が0である（相関がない）」という仮説、つまり本当は成立してほしくない帰無仮説の検証の結果を示す（3）。成立する確率が低いほど回帰モデルとして意味がある。回帰分析時には有意水準をP <0.05（5%）と設定しているため、0.05以下であれば帰無仮説の成立の見込みは低いと言える。　表３では、P－値が0.002を示しており、回帰モデルとして意味があると判断する。米国統計学会がP－値によくある誤解や誤用に対し注意喚起しているが（4）、本稿の回帰モデルは、Rからも判断できるように、意味があると考える。　表４に全フェーズの回帰分析結果と評価を示す。Rは全フェーズで高い相関を示した。ただし、フェーズ4のRが0.768であり、他のフェーズと比べると低い値を示した。図５からも、時刻t =20～25までの機器Aの温度データと計算値の差異が大きいことがわかる。　この差異の原因としては、フェーズの分割数が挙げられる。事例では、下降傾向としてひとつのフェーズとしてまとめ、フェーズ4とした。しかし、例えば、時刻t =20～25の温度と時刻t =25～30の温度を別のフェーズにすることで、より機器Aのデータに近い計算パラメータを決定することができ、RやP－値が向上する可能性があると考える。4．むすび　本稿では、曲線的な温度変化のモデル化について言及した。モデル化の対象となる温度データに式を当てはめることが最終目的であるが、熱伝導といった条件を加味することで、式に意味をもたせることができたと考える。　本稿の事例は、ごく単純な温度曲線を例としており、基本的なアプローチ方法である。しかし、本稿の目的の根幹は「物理現象の数値解析を可能とするために数式化すること」であるため、他の事象をモデル化する際にも応用できる考え方であると言える。参考文献⑴ 御園生善尚、吉野　崇、北野考一、武元英夫：応用数学大要、養賢堂、1980⑵ 2015年度品質生産性向上セミナーQ-6 回帰分析のツールについて考える、2015、社内講座資料⑶ 東京大学教養学部統計学教室：統計学入門、東京大学出版会、2013⑷ American Statistical Association ReleasesStatement on Statistical Significance and P-Values,ASA Newshttps://www.amstat.org/newsroom/pressreleases/P-ValueStatement.pdf、参照日2016/9/20執筆者紹介橘田　悠2012年入社。入社以来、衛星シミュレータシステムの開発に携わる。表３　フェーズ1の回帰分析の評価結果（抜粋） 表４　全フェーズの回帰分析結果と評価＊１　Excelの分析ツールでは重回帰分析への拡張を意識して　　　重相関と表記されているが単回帰分析では相関係数に　　　一致する。