M&S技術の進化・深化 － 業務の中で見つけた共通性と類似性

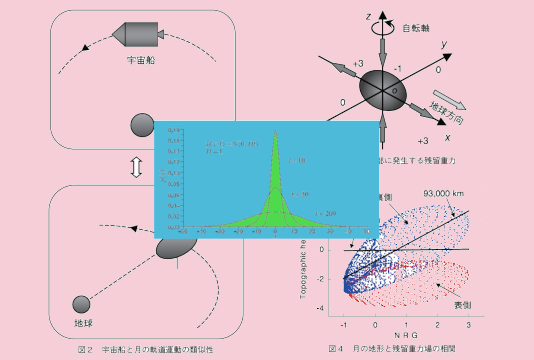
41 ＊鎌倉事業部　第一技術部
M&S技術の進化・深化 ̶ 業務の中で見つけた共通性と類似性
Evolution and Deepening of Modeling and Simulation：Commonalities and Similarities Found in Daily Work
矢田部　学＊　Manabu Yatabe
M&Sは工学、自然科学、社会科学などの広い分野を対象とし、数学モデルを作り上げることから出発する。そして、これらのモデルを用いてコンピュータシミュレーションを行い、新たな知見を得ることを目的の一つとする。対象分野が広範囲にわたるため、一見すると、モデルや数学的手法は全く異なるように見える。しかし、その中には共通性や類似性が存在する。それらに着目すると本質が見えてくる。本質の理解は、意外な新分野へ発展することが期待できる。本稿では、M&S業務の中で見つけた共通性と類似性について紹介する。　The aim of modeling and simulation（M&S）is to analyze systems in engineering, natural andsocial sciences, and so on. M&S starts from building mathematical models. Using the modelscomputer simulations are done, and the results provide new knowledge regarding the systems. Onthe surface, the models and techniques seem to be different from one another because of theirextensiveness. However there exist commonalities and similarities, which reveal the essence of themodels. Understanding their nature is expected to develop new fields. This report mentions thecommonalities and similarities found in daily work.
1．まえがき
　モデルは興味の対象の特徴を単純化したものである。ソフトウェアを用いたシミュレーションは数理モデルに基づいて実施され、新たな知見を得ることが目的の一つである。例えば、工学分野ではシステム設計の段階で、システムの最適化や予期せぬ障害の回避を目的としてシミュレーションによる検討が行われる（1）。今日、数理モデルとコンピュータシミュレーションを統合した分野はM&S（Modeling and Simulation）と言われる。　当社におけるM&S技術の原点は宇宙・防衛分野におけるエンジニアリング業務と考えられる。ロケットやミサイルの誘導・制御、宇宙空間や超音速などの特殊な環境における熱・構造解析、軍事オペレーションズ・リサーチなどは、工学や数学・物理の基礎知識が必要になる。このため、当社におけるM&S業務の根底には、表面に現れているIT技術の下に、数式を基礎とした仕事のやり方が存在する。　M&Sという用語は漠然としていて具体的にイメージし難いが、大別すると以下の手法が考えられる。⒜　ゼロから数学モデルを定式化してプロトタイプ的なモデルを作り解析を実施⒝　確立されたモデリング手法やシミュレーション・ツールを用いて大規模で緻密なモデルにより解析を実施　本稿では、表舞台に出ることが少ない「社内の隙間産業」的な⒜のタイプのM&S業務に視点をおき、そこで見出された数理モデルの共通性と類似性について述べる。隙間産業と言っても卑下するものではなく、基本原理からの理解を出発点としているため、物事の本質が見えてくるというメリットがある。本質の理解は、確かな仕事の基礎となり、競合他社との差別化につながり、意外な新分野へ発展することも期待できる。2．数理モデルの中にある共通性と類似性2.1　宇宙・防衛の業務に登場する方程式から　業務の中には様々な方程式が登場する。しかし、本質に気付けば共通性・類似性が見えてくる。例えば、宇宙分野のロケット・衛星の運動解析では運動方程式が基本となる。ここで、は質量、は位置、は力である。これは時間に関する２階の微分方程式である。　一方、防衛分野では兵力や戦闘能力を検討するオペレ　MSS技報・Vol.22 42が一つの方法と考えられる。以下は、当時の担当者がゼロの状態からスタートして、金融工学の先駆けとなったBlack-Scholes方程式に到達するまでの概要である。　金融工学は株価変動などのランダム性をモデルに取り入れるために確率過程を基礎に置く。確率過程では確率分布を規定するパラメータが時間的に変化する。例えば、平均がで分散がの正規分布の確率密度関数はと表されるが、確率過程では確率密度関数を支配するパラメータとが時間とともにランダムに変動し生起確率に影響を及ぼす。つまり、時間ごとに確率密度関数が異なる。その結果、実現値を与える確率変数が時間的に変化する。当時、このあたりを入り口として金融工学の理解を試みた。　金融工学に登場する確率過程はWiener過程である。これは水中に浮遊する微粒子が水分子と衝突してジグザグ運動するBrown運動の数学モデルである。株価などの金融商品の価値はWiener過程に従って変動すると考える。Wiener過程の確率密度関数は、ランダムウォークを記述するFokker-Planck方程式を出発点とし、この方程式に運動の対称性を仮定した拡散方程式の解として得られる（5）。時刻における粒子の位置をとすると確率密度関数はのように表される。ここで、は拡散係数である。　上式の形より、Wiener過程の確率密度関数は平均がで分散がの正規分布に従うことが分かる。このため、正規分布の広がりを表す標準偏差は　　　　 となり、時間とともに正規分布の山の高さは低くなり裾野が広がっていく（図１）。これを参考にして、Wiener過程の時間の変化をとする。ただし、は標準正規分布に従うとする。このようにすると、あたりのの分散がとなる。　株価などの金融商品は、短い期間で見るとWiener過程に従い平均値まわりを「ウロウロ」しているが、長期的にはある傾向（トレンド）をもって増加すると考えられる。そこで、株価の時間の変動を、とを定数としてとモデル化する。右辺の第１項のは株価の長期のーションズ・リサーチに関連してLanchester方程式が登場する（2）（3）。これは時間に関する１階の連立微分方程式でである。ここで、はR軍の兵力、はＢ軍の兵力、はＢ軍の単位兵力当たりの戦闘能力、はR軍の単位兵力当たりの戦闘能力である。　運動方程式とLanchester方程式は、一見すると異なるように見える。しかし、速度を取り出しとすると、運動方程式は１階の連立微分方程式となり、Lanchester方程式に類似した形式で表される。　更に、運動方程式もLanchester方程式も、状態量を導入してとすると、共通な形の方程式に表すことができる。右辺のは任意の関数である。M&S業務では、数値計算を行い結果を考察することが目的の一つであるが、この形の方程式は、常微分方程式の数値解法として、Euler法やRunge-Kutta法などが確立されている（4）。　このように、運動方程式とLanchester方程式は共通の手法で解くことできる。つまり、業務の中に共通性・類似性を見出すことは異なる分野の業務を行うときの手掛かりとなることがある。2.2　Brown運動から金融工学へ　欧米流の金融工学が注目され金融ビッグバンが騒がれていた1997年頃、当社においても「金融工学とは如何なるものか」を調査し新規事業を模索することになった。金融経済に弱い理系出身者が金融分野を理解することは困難が予想されるが、何とかして金融工学への入り口を見出す必要ある。このような場合、「経験分野との類似性」を金融工学の中に見出し、それを入り口とすること432.3　ISS内の微小重力環境からの発想̶月の形状と歴史　国際宇宙ステーション（ISS：International SpaceStation）で行う宇宙実験のために微小重力環境を解析していたときに気付いた類似性について紹介する。　宇宙実験は理想的には無重力を想定しているが、搭載機器の振動などによる擾乱を除いても、一般にISS内部は無重力ではなく微小重力場が存在する。この微小重力場は次のように説明できる。特定の面を地球方向に向けて軌道運動している宇宙船を考える。宇宙船は回転座標系と見なされるため遠心力が現れる。宇宙船の重心では地球の引力と遠心力が釣り合い重力はゼロになる。他方、重心から外れた位置では引力と遠心力の釣り合いが崩れて微小な重力が残ることになる（重心より地球側：引力＞遠心力、重心より反地球側：遠心力＞引力）。この意味で、この微小重力場は「残留加速度」（10）、「残留重力」（11）とも言われる。　問題の本質に気付けば、この「ISS内の微小重力環境」は、意外な方向に発展する。地球の衛星である月の運動を考える。月は同じ面を地球に向けて軌道運動している。つまり、月の軌道運動は上で述べた宇宙船の運動に類似していると見なされる（図２）。　これより、月の内部には宇宙船と同じ残留重力場が発生する。これは月の形状に影響を与えるはずである。地球に向かって軸、南極から北極に向かって軸を、それらと右手系をなすように軸をとると、この残留重力の分布は、比例定数を除くとのように表される。３つの軸方向の大きさの割合はとなる。残留重力は地球方向に＋３（伸び）、極軸方向に－１（縮み）の割合で作用変化を、第２項は短い期間の平均値まわりの変動を表す。この方程式は確率微分方程式と言われるものであり、方程式の中にのような確率過程の要素が含まれる。これよりとなるが、右辺の第２項は発散する。つまり、Brown運動のようにランダムに変動する現象は、滑らかな関数を扱う通常の解析学の範疇にないことを意味する。ランダムに変動する現象を扱うには伊藤清が生み出した確率解析学が必要である。金融工学では、その中に登場する「伊藤の補題（レンマ）」が重要な役割をはたす。　ランダムに変動する株価とそれに依存する金融派生商品（デリバティブ）からなるポートフォリオを考える。それより、株価の変動を表す式と伊藤の補題を用いて、確率的な変動分（リスク）を除くと、デリバティブの価格を記述するBlack-Scholes方程式に到達する。リスクの要因を除いたため、方程式の中には無リスク利子率が現れている。この方程式を境界値問題として解くことにより、ヨーロッパタイプ（満期日のみ行使可能）のコール・オプション（買う権利）やプット・オプション（売る権利）の価格評価モデルが得られる。　当時、Black-Scholes方程式に関する情報は少数であった（6）（7）（8）。現場における「金融工学との挌闘」は当時の技報の中に見ることができる（9）。　現時点において、金融工学は事業になっていない。しかし、金融工学を理解する過程で得られた数学的なノウハウは宇宙・防衛分野で使われるKalmanフィルタや防衛分野の捜索モデルなどの確率やランダム現象の絡んだ仕事の中に生かされている。図１　Wiener過程の確率密度関数の時間変化MSS技報・Vol.22 44　このように類似性に着目すると、日常の業務の中に意外なテーマを見つけることも可能なのである。その相乗効果として、本来の業務の理解は「深化」するのである。2.4　ロボットアームに潜んでいた意外性　　 ̶電磁場と回転座標系の力学の類似性　宇宙機に搭載するロボットアーム（マニピュレータ）の運動方程式を検討する業務の中で見つけた類似性について述べる。　ロボットアームは複数のリンクで構成されている。内側のリンクに対して外側のリンクがヒンジ回りに回転すると、外側のリンクに固定された座標系は回転座標系と見なされ、遠心力やCoriolis力が現れる。ここで、回転座標系の運動方程式を眺めていると、以下のような興味深い事実に気付く。　角速度で回転している質点系を考える。その中の１つの質量の質点に着目する。回転座標系で記述した運動方程式はする。公転軌道の方向には０となり、残留重力は作用しない（図３）。　この残留重力の割合（NRG：Normalized ResidualGravity）と月の形状の関係をプロットしたものが図４である。図に示すようにNRGと月の地形は相関がある。この相関は月の表側と裏側で異なる。裏側の地形の相関は表側より強い。この相違は月の歴史により説明できる。原始の月は表面がマグマオーシャンで覆われていたと考えられている。それが固化して原始地殻ができたとき、当時の残留重力場に適合する平衡形状であったと考えられる。その後、表側で玄武岩質マグマの噴出により海が形成され、原始地殻が保存していた固化当時の残留重力の情報が失われてしまった。このため、月の表側の地形では裏側に比べて相関が弱くなる（12）。　月の地形データと残留重力の大きさの理論値を用いて、月が固化したときの地球と月の距離を見積ると93,000kmとなった。現在の地球と月の距離は384,400kmである。これは当時に比べて地球の自転が遅くなり、地球－月系の角運動量を保存するために地球から月が離れていった結果である。図３　月の内部に発生する残留重力図２　宇宙船と月の軌道運動の類似性図４　月の地形と残留重力場の相関45程式に類似した方程式が得られる（13）。上の３つの方程式は数学的に導出できる。最後の方程式は物理現象からの推測である。　ここで述べた内容は推論が入り未完成であるが、今回の特集のテーマである「進化」の途中にある例として紹介した。ゼロから数理モデルを作り上げるとき、このような試行錯誤が行なわれる。その多くは未完成のまま残るが、別の業務にその経験が生きるのである。3．既存業務からの発展̶「戦いのモデル」から「生態系のモデル」へ　第２章では実務の中で見出した共通性や類似性ついて紹介した。ここでは方程式の共通な形式を基にして、既存分野を新規分野へ発展させる手掛りについて考える。　運動方程式とLanchester方程式は第2.1節で述べたように共通な形で表すことができる。この方程式で表されるシステムは「力学系」と言われる。その呼び方は力学（運動方程式）に由来し、相互作用する個の要素からなる状態量の時間変化を記述する。　分かりやすいようにの場合を考えてとする。これは、との「競争のモデル」と考えることができる（図６）。そのような見方をすると、運動方程式よりは、戦いを記述したLanchester方程式のほうがイメージしやすい。　競争は「生態系の共存モデル」として使える。例えば、２種類の生物がある地域に生息していて、一方が他方を餌にしている場合などである。　この種の問題は「サメと小魚」の漁獲高を説明する問題として定式化されている（Lotka-Volterraモデル）（14）（15）。である。ただし、ドットは時間微分、は位置、は速度、は他の質点からの作用（引力）である。ここで、とおき、運動方程式をのように書き表す。　他方、電場、磁場の中で運動する荷電粒子（質量、電荷）にはLorentz力が作用し、運動方程式はと書ける。　ここで、回転座標系と電磁場の運動方程式内に現れるを比較（数式のパターン認識）するとなる対応に気付く。電磁場を決めるの基礎方程式はMaxwell方程式である。このことより、回転座標系のに関しても「同様な方程式が存在するか？」という疑問が浮かぶ。実際に、発散と回転をに作用させると、図５に示すようにMaxwell方図５　回転座標系における場の方程式は存在するか？MSS技報・Vol.22 46のようになる。被食者（青）が増殖すると餌が増えて捕食者（赤）も増加する。捕食者が増加すると食べられて被食者は減少する。その結果、食べる餌が無くなり捕食者も減少する。捕食者が減少すると被食者は増殖する。以降、これを周期的に繰り返す。この周期性は、もとの方程式でとしたとき、平衡点が存在することからも予想できる。　ここでは状態量の要素が２つの場合を考えたが、それより多い場合を考えることも可能である。Lotka-Volterraモデルは、昨今話題に挙がる環境問題のモデル化の手掛りになると考えられる。4．むすび　当社のM&S技術は宇宙・防衛分野のエンジニアリング業務を原点としている。その根底には数式を基礎とした仕事のやり方がある。現在では、それはIT技術の陰に隠れて表に現れることは少ない。しかし、解析ツールのような数式を基礎におくソフトウェアは、表向きのIT技術が立派でも、根底にある数式がいい加減では使い物にならない。意味を理解せずに単に公式を組み合わせたような貧弱な計算では正しい結果に到達することは難しい。　今回の特集号「技術の進化・深化」の執筆を依頼されたとき、最初は断るつもりでいた。自分が担当してきた「泥臭い数式」を基礎とする仕事は、社内では隙間産業と見なされ、期待されている技術とはかけ離れていると思えたからである。　昨年と今年、宇宙・防衛分野に関係した基礎的な勉強会（Kalmanフィルタ、クォータニオン、軌道力学）を開催したが、毎回20人前後の有志が集まった。参加者は第１次世界大戦中、アドリア海では漁業が中止された。そのために小魚が増殖することが期待された。ところが戦争が終わって漁業を再開すると、小魚は減りサメなどの肉食魚が増えていた。　これを説明するために、イタリアの数学者Volterraは以下のようにモデル化した。　・捕食者（サメ）がいないとき被食者（小魚）は自然に増殖　・捕食者に遭遇すると被食者は食べられて減少　・捕食者は寿命により自然に減少　・捕食者は被食者を食べて子孫が増加これを数式で表現するとのようになる。ただしである。　１番目の方程式のは被食者の増殖率の減少を意味する。これは捕食者に食べられて被食者が減少する効果である。また、２番目の方程式のは捕捉者の死滅率の減少を意味する。これは被食者を食べて捕食者が増加する効果である。つまり、相手の存在により、本来の増殖率と死滅率は影響を受けると考えてモデル化している。　この方程式を解くと被食者と捕食者の時間推移は図７図６　競争のモデル図７　被食者と捕食者の推移47ウォークとブラウン運動、日科技連（1994）⑻　辰巳　憲一：デリバティブと新金融商品の数学、東洋経済新報社（1995）⑼　矢田部　学・小島　智：確率過程から見た株価、MSS技報、Vol.12、1～7（1999）⑽　狼　嘉彰・松永　三郎・井沢　克彦：地球低軌道上スペースクラフト内における残留加速度の数値シミュレーションと評価、日本航空宇宙学会誌、42号、251～258（1994）⑾　矢田部　学：軌道上システム内における残留重力場、MSS技報、Vol.10、1～5（1997）⑿　Yatabe, M.：The Lunar Shape Examined by theResidual Gravity Field, J. Geod. Soc. Jpn, Vol.46,203～222（2000）⒀　矢田部　学：回転座標系の力学と電磁場のアナロジー、MSS技報、Vol.13、76～79（2001）⒁　丹羽　敏雄：数学は世界を解明できるか、中公新書（1999）⒂　Abraham, R. and Show, C.：Dynamics－theGeometry of Behavior, Aerial Press（1982）「基礎から理解することの重要性」を実務をとおして認識していた。また、編集者からは、当社では「数式を基本にした仕事のやり方」が伝承されていることを示して欲しいと言われた。執筆することにしたのは、それらの理由による。　世の中の風潮に従うと効率化が優先され手間のかかるやり方は敬遠される。しかし、基本に立ち返りゼロからスタートすると本質が見えてくる。その結果、一見すると異なる分野の中に共通性・類似性を見出すことができ、意外な方向に進化・深化が起こるのである。これは何もM&Sに限ったことではない。参考文献⑴　Maria, A.：Introduction to Modeling andSimulation, Proceedings of the 1997 WinterSimulation Conference, 7～13（1997）⑵　飯田　耕司：戦闘の科学　軍事ORの理論、三恵社（2005）⑶　Przemieniecki, J. S.：Mathematical Methods inDefense Analysis, AIAA（2000）⑷　Woan, G.：The Cambridge Handbook of PhysicsFormulas, Cambridge Univ. Press（2000）⑸　中川　正雄・真壁　利明：理工系基礎　確率過程、培風館（1987）⑹　三菱銀行商品開発室：ジョン・ハル=ファイナンシャルエンジニアリング金融派生商品開発入門、きんざい（1992）⑺　木島　正明：ファイナンス工学入門第I部ランダム