戦略の数理－ランチェスターの法則

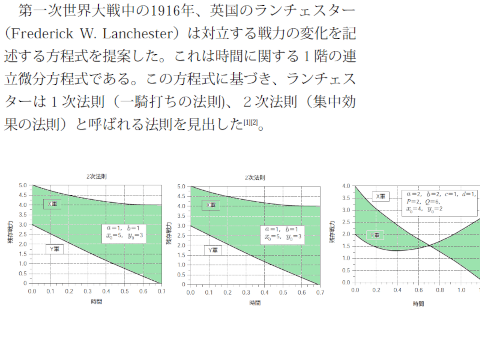
戦略の数理―ランチェスターの法則
Mathematical Model of Strategy：Lanchester’s Laws
矢田部　学＊
Manabu Yatabe
第一次世界大戦中、ランチェスターは敵対する二つの戦力の状態を考察するための微分方程式を提案した。その方程式から導かれる法則は戦略の指針を示し、軍事的な作戦ばかりでなく、今日ではビジネスにおける経営戦略にも応用されている。本レポートではランチェスターの法則について一つの解説を試みる。
Lanchester formulated differential equations to describe two opposed war powers during the First World War. Laws derived from the equations indicate guidelines for battle plans. Nowadays the laws are applied to not only military operations but also business strategy. We review the fundamental concept of the Lanchester’s laws in this report.
1．まえがき第一次世界大戦中の1916年、英国のランチェスター（Frederick W. Lanchester）は対立する戦力の変化を記述する方程式を提案した。これは時間に関する１階の連立微分方程式である。この方程式に基づき、ランチェスターは１次法則（一騎打ちの法則)、２次法則（集中効果の法則）と呼ばれる法則を見出した[1][2]。ランチェスターの方程式・法則は軍事を分析するために提唱されたものであるが、今日ではその考え方は経営戦略にも適用されている[3]。これはビジネスの世界も企業の生存競争と考えれば当然のことであろう。ランチェスターの方程式は比較的簡単な方程式であるため、その考え方や解法は、様々な現象（人口問題、生存競争、環境問題、在庫状況など）のモデリングやシミュレーションに参考になると考えられる。そこで、本レポートでは、ランチェスター方程式の考え方や解析的な解法などについてまとめた私的メモの一部を紹介する。2．基本法則ランチェスターの二つの基本法則である、１次法則と２次法則について述べる。2.1 １次法則ランチェスターの１次法則は「一騎打ちの法則」とも呼ばれ以下を前提とする。・一度に一人の相手と戦う「一騎打ち」を想定・つまり、近距離の戦いをモデル化・戦力の減少は相手の武器性能に比例これらは戦国時代の戦い方のイメージで、軍と軍の戦力は以下の方程式で記述される。（1）初期条件： （2）ただし、：X軍の戦力数：Y軍の戦力数：Y軍の武器性能：X軍の武器性能（1）からわかるようにとは独立である。したがって、それぞれを積分して、時刻でのX軍とY軍の残存戦力は以下のようになる。（3）これらより、t を消去すると（4）ただし、：武器性能比これがランチェスターの１次法則である。X軍とY軍の初期戦力を、それぞれおよびとする。また、X軍とY軍の武器性能を、それぞれおよびとする。つまり、初期戦力ではY軍が勝っているが武器性能はX軍のほうが高い。この場合の（1）の解（3）をプロットしたものが図１である。これより、初期戦力が劣っていても、高性能の武器を使用す戦略の数理―ランチェスターの法則Mathematical Model of Strategy：Lanchester’s Laws矢田部　学＊Manabu Yatabe第一次世界大戦中、ランチェスターは敵対する二つの戦力の状態を考察するための微分方程式を提案した。その方程式から導かれる法則は戦略の指針を示し、軍事的な作戦ばかりでなく、今日ではビジネスにおける経営戦略にも応用されている。本レポートではランチェスターの法則について一つの解説を試みる。Lanchester formulated differential equations to describe two opposed war powers during the FirstWorld War. Laws derived from the equations indicate guidelines for battle plans. Nowadays the lawsare applied to not only military operations but also business strategy. We review the fundamentalconcept of the Lanchester’s laws in this report.MSS技報・Vol.19 40れば勝つという結論になる。X軍の残存戦力は１次法則（4）より、以下のように算出できる。同じ武器性能比であっても、異なる武器性能とではY軍の戦力がゼロになるまでの時間が異なることが、式（3）よりわかる。2.2 ２次法則ランチェスターの２次法則は「集中効果の法則」とも呼ばれ以下を前提とする。・一人で複数の敵を同時に攻撃可能・つまり、遠距離攻撃可能な武器を使用した場合に相当・戦力の減少は相手の武器性能と戦力の積に比例これらは近代の戦争のイメージで、X軍とY軍の戦力は以下の方程式で記述される。（5）初期条件： （6）ただし、：X軍の戦力数：Y軍の戦力数：Y軍の武器性能：X軍の武器性能第１式第２式の結果を時間で積分して（ ：積分定数）（6）を適応すると、なので（7）ただし、：武器性能比これがランチェスターの２次法則である。また、初期条件（6）で（5）を解析的に解くと、時刻でのX軍とY軍の残存戦力は以下のようになる（導出は付録参照)。（8）２次法則についても１次法則と同様に考えることができる。X軍とY軍の初期戦力を、それぞれおよび、X軍とY軍の武器性能を、それぞれおよびとする。この場合の（5）の解（8）をプロットしたものが図２である。X軍の残存戦力は２次法則（7）より、以下のように算出できる。１次法則と同様に、同じ武器性能比であっても、異なる武器性能では戦いの終了までの時間（一方の戦力がゼロ）になるまでの時間が異なることが、式（8）よりわかる。2.3 １次法則と２次法則の比較以下の条件のもとに、１次法則と２次法則を比較する。・両軍の武器性能は同じとする（武器性能比： ）・初期戦力はX軍、Y軍でX軍優勢とするこれらを式（4）の１次法則と式（7）の２次法則に適用する。１次法則：２次法則：765432100.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5時間残存戦力Y軍X軍􀁟＝1，􀁠＝20＝5， 0＝7図１　１次法則765432100.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7時間残存戦力Y軍X軍＝1， ＝30＝5， 0＝7図２　２次法則41技術解説つまり、戦力優勢なX軍は２次法則で戦ったほうが、残存が大きくなる。他方、戦力劣性のY軍は１次法則で戦ったほうがX軍に大きな被害を与えることができる（図３参照）。これはビジネスにおける経営戦略についても同様であると考えられる。つまり、大企業は多角経営で２次法則的に経営を行ったほうがよく、中小企業は特定分野に特化して１次法則的に経営を行ったほうが、業界にインパクトを与えることができる。3．基本法則の拡張基本法則を拡張して、戦力の分割と補給の効果を取り入れた以下の方程式を考える。（9）ただし、：X軍の戦力数：Y軍の戦力数：Y軍の武器性能：X軍の武器性能：作戦で生じるX軍の戦力減少：作戦で生じるY軍の戦力減少：X軍の戦力増加（補給率）：Y軍の戦力増加（補給率）初期条件： で（9）を解析的に解くと、時刻でのX軍とY軍の残存戦力は以下のようになる（導出は付録参照）。（10）ただし、（11）X軍とY軍の初期戦力をおよびとし、X軍とY軍の武器性能は等しくおよびとする。作戦で生じるX軍とY軍の戦力減少は等しくおよびとする。また、X軍の補給率を、Y軍のそれをとする。この場合の（9）の解（10）をプロットしたものが図４である。初期戦力が劣っていても、戦力の補給率を大きくすると勝つことが可能となる。5.04.54.03.01.53.52.52.01.00.500.0 0.5 1.0 1.5 2.0 2.5 3.0時間残存戦力5.04.54.03.01.53.52.52.01.00.500.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7時間1次法則2次法則残存戦力Y軍X軍α＝1，β＝10＝5， 0＝3＝1， ＝10＝5， 0＝3Y軍X軍図３　１次法則と２次法則4.03.53.02.52.01.51.00.50.00.0 0.2 0.4 0.6 0.8 1.0 1.2時間残存戦力Y軍X軍＝2， ＝2，c＝1，d＝1，P＝2，Q＝6，0＝4， 0＝2図４　戦力分割と補給の効果を考慮したランチェスターの法則MSS技報・Vol.19 424．簡単な応用例ランチェスター方程式の簡単な応用を示す。X国とY国の戦いをモデル化する。両国の戦力は海軍と空軍からなるものとする。これらの戦力が同時に戦闘を開始して、どちらか一方の国の戦力がゼロになるまで戦いを続けるものとする。これを以下の方程式で表す。（12）ただし、：X国海軍の戦力：X国空軍の戦力：Y国海軍の戦力：Y国空軍の戦力：X国海軍に対するY国海軍の武器性能：X国海軍に対するY国空軍の武器性能：X国空軍に対するY国海軍の武器性能：X国空軍に対するY国空軍の武器性能：Y国海軍に対するX国海軍の武器性能：Y国海軍に対するX国空軍の武器性能：Y国空軍に対するX国海軍の武器性能：Y国空軍に対するX国空軍の武器性能パラメーターとして以下を与える。つまり、武器性能はY国のほうがX国より勝っている。また、初期戦力はとする。式（12）を４次のルンゲ－クッタ法で数値的に積分したものを図５に示す。X国の空軍が全滅し、その後、海軍も全滅する。最終的にY国が勝つ結果となった。5．むすび以上、ランチェスターの方程式とそれから導かれる法則について述べた。これらの考え方は比較的簡単である。そのために数理的なモデルリングが未開発の分野の考察を開始するときには参考になる。そのような機会があれば積極的にランチェスターの考え方を適用したいと考えている。参考文献[1] 金吉雅人：ランチェスター方程式の改良と動向，MSS技報，Vol.1，pp.56-60，1989[2] 飯田耕司：戦闘の科学　軍事OR の理論，三恵社，2005[3] 福永雅文：ランチェスター戦略「一点突破」の法則，日本実業出版社，2007付録　厳密解の導出A ２次法則の方程式式（5）の第１式をで微分して第２式を代入するとこの方程式の一般解は、とを定数として（A1）初期条件（6）を代入すると（A2）（5）の第１式と（A1）より初期条件（6）を代入して（A3）（A2）と（A3）よりこれらを（A1）に代入すると（8）の第１式が得られる。また、（5）の第２式をで積分すると、を定数としてこれに（8）の第１式を代入し、初期条件（6）を適用するととなり、（8）の第２式が得られる。5.04.54.03.01.53.52.52.01.00.500.00 0.05 0.10 0.15 0.20 0.25 0.30時間残存戦力X国海軍X国空軍Y国空軍Y国海軍図５　X国とY国の戦いB 戦力分割と補給を考慮した方程式式（9）と初期条件を行列で表現すると（B1）（B2）ただし、（B1）の両辺に左からを乗じ、時間で積分して、初期条件（B2）を適用すると（B3）ここで、行列を対角化して、（B1）を独立な二つの方程式にすることを考える。行列の固有値と固有ベクトルはに対して　に対して　なので、行列を対角化する行列は（B4）であり、その逆行列は（B5）と表される。ただし、、およびは（11）に与えられている。これより、は（B6）と対角化される。他方、を単位行列としてなのでである。これを（B4）、（B5）および（B6）を用いて具体的に計算するとしたがって、これらを（B3）に代入すると（10）が得られる。43技術解説