テクノロジー
技術レポート:アーカイブ
Category:ロケット・宇宙機・人工衛星開発
クォータニオン計算便利ノート
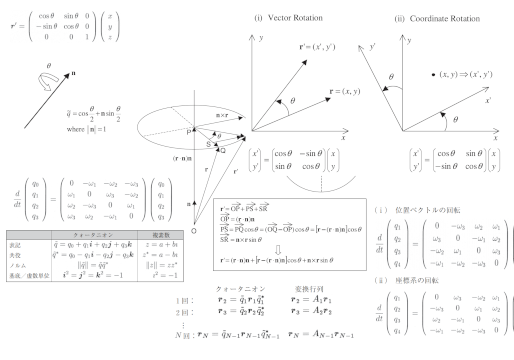
クォータニオンは回転軸(ベクトル)と回転角(スカラー)よりなる4成分で3次元空間の回転を表現する。クォータニオン表現ではオイラー角による回転表現で生じるような特異点が存在しない。そのため、宇宙・防衛分野における飛翔体の姿勢計算には、伝統的にクォータニオンが用いられてきた。また、最近では3次元コンピューターグラフィックの分野でも物体を表示するためにクォータニオンが使用されている。クォータニオンの定義には、大別すると二つの流儀がある。そのために時々混乱が生じる。本レポートでは飛翔体の姿勢計算に有用なクォータニオンの公式を整理する。
参考情報:
クォータニオン計算便利ノート *鎌倉事業部 第一技術部(博士(理学)) MSS技報・Vol.18 29技術論文クォータニオン計算便利ノートHandy Note for Quaternions矢田部 学*Manabu Yatabe クォータニオンは回転軸(ベクトル)と回転角(スカラー)よりなる4成分で3次元空間の回転を表現する。クォータニオン表現ではオイラー角による回転表現で生じるような特異点が存在しない。そのため、宇宙・防衛分野における飛翔体の姿勢計算には、伝統的にクォータニオンが用いられてきた。また、最近では3次元コンピューターグラフィックの分野でも物体を表示するためにクォータニオンが使用されている。クォータニオンの定義には、大別すると二つの流儀がある。そのために時々混乱が生じる。本レポートでは飛翔体の姿勢計算に有用なクォータニオンの公式を整理する。 Quaternions describe rotations in the 3-dimensional space by using four components, whichconsist of a rotation axis vector and an angle.The quantities can avoid such singularities as Eulerangles have.For that reason, the quaternion methods have been traditionally used for attitudedeterminations of flying objects in aerospace and defense areas.Recently the quaternions are used in3-dimensional computer graphics to represent objects.There are generally two different definitions ofthe quaternions, which sometimes lead to confusion.We summarize useful formulas for the attitudecalculations of the fling objects in this report. 1.まえがきクォータニオンはアイルランドの数学者ハミルトン(William Rowan Hamilton)により考案され、今日のベクトル解析に代わる手法として、19世紀の数理物理学で用いられた。当時の電磁気学に関する論文の多くはクォータニオンによる表現になっている(1)。20世紀になるとギブス(Josiah Willard Gibbs)によるベクトル解析が主流となり、クォータニオン計算は少なくなった。筆者の知る限りでは、クォータニオン計算で記述されている教科書は、堀による「天体力学講義(1988)」くらいである(2)。クォータニオンはベクトル計算の代替手法として用いられることは少ないが、飛翔体の姿勢計算では頻繁に使用される(3)(4)(5)(6)。これはオイラー角のような特異点が存在しない理由による。また、最近では3次元コンピューターグラフィックの分野でも物体を表示するためにクォータニオンが使用される(5)(7)。以前、MSS技報でクォータニオンについての解説を試みた(8)。そのときは手元にある断片的な公式を整理して体系化することを目的とした。その後、いくつかの宇宙機の姿勢計算に関する業務を経験し有用な公式を再整理した。本レポートでは、飛翔体の姿勢計算に関する技術資料や論文を読む際に便利なクォータニオンの公式に関する私的メモの一部を紹介する。2.記号本レポートで使用する記号についてまとめる。蘆ベクトルベクトルはボールド体で表し、とくに断りがない限り、その成分を添え字1,2,3で表す。例えばと表記する。蘆クォータニオンクォータニオンは上にチルダをつけて表し、その成分を0,1,2,3で表す。また、スカラー部とベクトル部に分けて表すこともある。例えばと表記する。または、ベクトル部を、スカラー部をで表しと表記する。蘆スカラー積二つのベクトルとのスカラー積(内積)はドットで表す。・30技術論文蘆ベクトル積二つのベクトルとのベクトル積(外積)はクロスで表す。3.クォータニオン(四元数)とは今日のベクトル解析では、ベクトルとの積の定義が二種類ある(ギブス流):(スカラー積)および (ベクトル積)これらより、以下の積を定義する(ハミルトン流):盧この定義により二つのベクトルの積はスカラー部(- )とベクトル部( )よりなる拡張された数になっている。この拡張された数をクォータニオン(quaternion)または四元数(しげんすう)という。なお、二つのベクトルの積は非可換である( )。直交座標系軸、軸、軸の基底ベクトルをそれぞれ、、とすると盧より盪クォータニオンはスカラー部- とベクトル部より成り立っている。3.1 クォータニオンスカラー部を、直交座標系でのベクトル部をとするとクォータニオンは蘯ここで、とおいた。3.2 共役クォータニオンクォータニオンのベクトル部の符号を反転したものを共役クォータニオンという。盻3.3 クォータニオン積二つのクォータニオンとの積は、盧より以下のようになる。眈これを、とのクォータニオン積(quaternionproduct)という。クォータニオン積はベクトル部とスカラー部より構成されるから、クォータニオンである。また、クォータニオン積は非可換である( )。クォータニオン積を行列で表記するととなる。3.4 ノルム共役クォータニオンを用いるとノルムが定義できる。クォータニオンのノルムは眇二つのクォータニオンとについてが成り立つのでノルムは正の平方根なので眄が成り立つ。3.5 逆クォータニオンノルムを用いると逆クォータニオン眩を定義できる。この定義と眇より、であり、確かには逆クォータニオンであることが分かる。また、の単位クォータニオンは共役が逆クォータニオンになる。3.6 回転を表すクォータニオン単位ベクトルと回転角として、以下の特別なクォータニオンを考える(図1参照)。眤このノルムはである。このクォータニオンを用いて位置ベクトルと座標系の回転を表すことができる。(衢)座標系を空間に固定して位置ベクトルを回転する場合と(衫)点を空間に固定して座標系を回転する場合の変換式を以下に示す(図2参照)。(衢) (位置ベクトルの回転) 眞(衫) (座標系の回転) 眥×・×・×・×MSS技報・Vol.18 31式眞を具体的に評価すると以下のようになる。眦図3に示すような幾何学的な考察により、眞が位置ベクトルの回転を表すことが分かる。例えば軸まわりの回転を考えて、、およびを眞の右辺に代入するととなり、これは位置ベクトルの回転を表している(図2参照)。同様に、点を固定して座標系を回転する場合について式眥を具体的に評価すると眛となる。式眦と眛の違いは右辺のベクトル積の順序である。この違いが効いて、例えば軸まわりの回転ではとなり、確かに座標系の回転を表している(図2参照)。3.7 クォータニオン表現による変換行列位置ベクトルまたは座標系を回転したときの変換行列をクォータニオンの成分で表す。(衢) 位置ベクトルの回転式眞より眷として、クォータニオンの部分を展開すると、位置ベクトルをに変換する行列は眸となる。(衫) 座標系の回転同様に、式眥より睇として、座標系をに変換する行列は睚式眸と睚より、であることが分かる。ただし、は転置行列を意味する。また、とは直交行列であるから(単位行列)となる。3.8 回転の合成位置ベクトルまたは座標系に関して一連の回転を行ったときのクォータニオンと変換行列の合成について述べる。図2 位置ベクトルの回転と座標系の回転の違い(2次元)図1 回転を表すクォータニオン32技術論文(衢) 位置ベクトルの回転回の位置ベクトルの回転を行うとき、式眞と眷よりクォータニオン 変換行列1回: 2回: 回:なので、なるクォータニオンについて睨なる変換行列について睫となる。クォータニオンと変換行列の積の順序は同じである。(衫) 座標系の回転位置ベクトルの回転のときと同様に考える。回の座標系の回転を行うとき式眥と睇よりなるクォータニオンについて睛なる変換行列について睥となり、クォータニオンと変換行列の積の順序は逆である。3.9 クォータニオンの時間微分クォータニオンの時間微分について考える。(衢) 位置ベクトルの回転時刻のクォータニオンが後にになったとすると、睨よりが成り立つ。微小時間間の変化がまわりの微小角によるものとするとこれらよりが成り立つ。ここで、とすると睿ただし、とおいた。ここで、ベクトルとクォータニオンの積を盧に従って評価すると、睿は睾となる。これは位置ベクトルが角速度で回転するときのクォータニオンの時間変化を表す。(衫) 座標系の回転式睛を用いると、時刻のクォータニオンはとなり、(衢)と比較して積の順序が入れ代わる。同様図3 位置ベクトルの回転…MSS技報・Vol.18 33な手順で、座標系が角速度で回転するときのクォータニオンの時間変化は以下のようになる。睹3.10 複素数との対比虚数単位をとして、実部、虚部よりなる複素数瞎と比較すると、クォータニオンは複素数の拡張である超複素数(hyper-complex number)とみなすことができる。複素数との対比を考えるとクォータニオンの公式が理解しやすくなる。クォータニオンと複素数の対比を表1にまとめる。4.もう一つの定義これまで、蘯のようにスカラー部をに続いてベクトル部を書いてのようにクォータニオンを表記した。クォータニオンの定義にはもう一つの流儀がある。それは、ベクトル部に続いてスカラー部を書いてとする。これまで3節で述べてきた公式は、として、行列表記の対応する成分を置き換えることにより成り立つ。以下に、成分で表記する際に混乱が起きやすい公式をまとめる。4.1 クォータニオン積4.2 クォータニオン表現による変換行列(衢) 位置ベクトルの回転変換に対して(衫) 座標系の回転変換に対して4.3 クォータニオンの時間微分(衢) 位置ベクトルの回転(衫) 座標系の回転5.むすび飛翔体の姿勢計算で使用するクォータニオンの公式について整理した。クォータニオンの定義には、スカラー部とベクトル部の順序に二つの流儀がある。また、位置ベクトルを回転する場合と座標系を回転する場合では回転の符号が逆になる。このため、実作業において混乱が発生する。本レポートで整理した公式により、クォータニオン計算を行う際の混乱が減少するはずである。参考文献盧太田浩一:マクスウェル理論の基礎―相対論と電磁気学,東京大学出版会,2002盪堀 源一郎:天体力学講義,東京大学出版会,1988表1 クォータニオンと複素数の対比クォータニオン表記共役ノルム基底/虚数単位複素数34技術論文蘯Wertz,J.R.:Spacecraft Attitude Determinationand Control,Kluwer,1978盻Goldstein,H.:Classical Mechanics(2nd ed.),Addison Wesley,1980眈Kuipers,J.B.:Quaternions and Rotation Sequences,Princeton Univ. Press,1999眇狼嘉 彰,冨田信之,中須賀真一,松永三郎:宇宙ステーション入門,東京大学出版会,2002眄金谷一郎:3D-CGプログラマーのためのクォータニオン入門,工学社,2004眩矢田部 学:四元数による回転表現,MSS技報,Vol.9,pp.13-18,1995