テクノロジー
技術レポート:アーカイブ
Category:情報処理システム
目的物探知の確率モデル
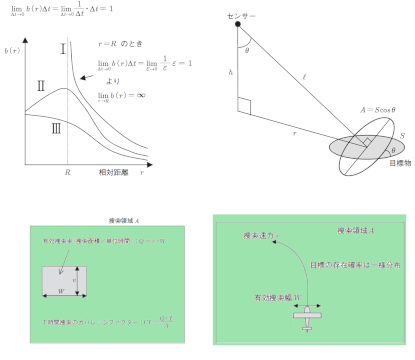
捜索理論は「潜水艦探し」を目的として第二次世界大戦中に基礎が築かれた。その理論は確率モデルをベースとして体系化されている。捜索理論はオペレーションズ・リサーチ(OR)の一分野とみなされる。戦後爆発的に発展した他のOR分野とは異なり、捜索理論は、その目的が特定の分野に限られていたために、少数派により研究されてきた。そのために、一般に知られることはあまりなかった。本レポートでは、捜索理論の基礎概念(探知確率、探知ポテンシャルなど)について概観する。
参考情報:
目的物探知の確率モデル *鎌倉事業部 第一技術部(博士(理学)) MSS技報・Vol.17 24目的物探知の確率モデルProbability Model for Detecting Objects矢田部 学*Manabu Yatabe 捜索理論は「潜水艦探し」を目的として第二次世界大戦中に基礎が築かれた。その理論は確率モデルをベースとして体系化されている。捜索理論はオペレーションズ・リサーチ(OR)の一分野とみなされる。戦後爆発的に発展した他のOR分野とは異なり、捜索理論は、その目的が特定の分野に限られていたために、少数派により研究されてきた。そのために、一般に知られることはあまりなかった。本レポートでは、捜索理論の基礎概念(探知確率、探知ポテンシャルなど)について概観する。 A foundation of“search theory”was built for the purpose of“submarine hunting”during WorldWar II.The theory is formulated by probability models and is regarded as branch of operationsresearch(OR).In the postwar period, many areas of the OR have been developed explosively.On thecontrary, the search theory has been researched by minority expert groups due to the purposerestricted to specific areas.Therefore it has been little known to the general public.We review thefundamental concepts(detection probabilities, potentials, etc.)of the search theory in this report. 1.まえがき 長い間、人類は生活の中で「物探し」という行為を繰り返してきた。物探しの基本は「ありそうな所を探せ」である。しかし、これが科学として体系化されたのは最近のことである。物探しの理論、すなわち捜索理論はオペレーションズ・リサーチ(OR)の一分野として、第二次世界大戦中の「潜水艦探し」から生まれ、それは確率モデルに基づいて体系化された(1)。米国はこの理論に基づき独海軍のUボート(独語:潜水艦das U-Boot,Unterseeboot)の捜索に大きな成果をあげた。戦後まもなく、この研究内容は出版され、この分野の古典となっている(2)。その後、捜索理論は、その研究目的が軍事などの特定分野に限定されていたため、少数派により研究されてきた。そのために、捜索理論は他のOR関連分野(数理計画、統計・データ解析、待ち行列、ゲーム理論など)が成し遂げたような爆発的発展から取り残された。この事情はわが国においても同様で、孤立した分野という感がある。現時点で、入手可能な書籍は、飯田・宝崎による「改訂捜索理論(2003)」くらいである(3)。これは、捜索理論を数理科学として体系化し紹介したもので、この分野の内容を「ちょっと知る」のに便利で貴重な本である。他方、捜索理論の適用範囲は「物探し問題」であり、日常生活にも応用範囲が広いと考えられる。また、将来的に人類が地球上から宇宙空間などに活動範囲を広げた場合、新たな応用の可能性もある。今後、いろいろな分野に捜索理論が適用され、発展していくことが期待される。本稿では、筆者が文献(3)に基づいて、捜索センサーの探知確率や区域捜索など捜索理論の基礎概念について整理した私的メモの一部を紹介する。 2.捜索センサーの探知能力モデル 捜索センサーの探知能力を特徴づける概念について述べる。2.1 瞬間探知確率捜索センサーの能力は「センサーからどの程度離れた目標を、どの程度の確率で探知できるか」により評価される。センサーからの距離にある目標を、微小時間捜索したときの探知確率は捜索時間に比例すると考えて盧と記す。この比例定数は、単位時間当たりの探知確率を表し、「瞬間探知確率」という。「単位時間当たり」という表現には注意を要する。ならば、は単位時間当たりの探知確率である。しかし、これが1を超えると探知確率として25の意味を失う。つまり、盧の表現は微小な時間内で成り立つ。したがって、一般にの有限時間長の積分は確率の意味を持たない。なぜならば、有限時間で積分すると1を超えてしまうことが起こるからである。後で述べるように、この積分は「探知ポテンシャル」としての意味をもつ(第2.2節を参照)。瞬間探知確率を「距離-探知確率」で表す。典型的な場合を図1に示す。タイプIは距離内では確実に探知(確率1)される。タイプIIはセンサーの近傍では探知しにくく、距離で最大となる。そして、タイプIIIはセンサーの距離とともに探知確率が下がる。瞬間探知確率は、センサーが捜索空間を連続的に捜索する場合のモデルである。センサーが離散的な捜索を行なうときの探知確率を「瞥見(べっけん)探知確率」という。本稿は連続センサーに限定して、その考え方を述べる。したがって、この瞥見確率については、他の文献を参照されたい(例えば、飯田・宝崎、2003)(3)。距離-探知確率の数学的な表現を「発見法則」という。以下に、代表的な発見法則について述べる。2.1.1 完全定距離発見則目標-観測者間距離が以内では必ず探知し、より離れると探知しないとした距離-探知確率曲線を「完全定距離発見則」という。これは、図1のタイプIの極端な場合と考えられる。近距離における探知確率が大きなセンサーについてはこのモデルで近似できる。盪のとき、が微小時間について成り立つためにはである必要があるので蘯でなければならない。2.1.2 不完全定距離発見則微小時間の捜索で距離が以内では一定確率で探知し、より離れると探知しないとしたモデルを「不完全定距離発見則」という。これは図1のタイプIIIの極端な場合である。近距離の探知確率が小さいセンサーはこのモデルで近似できる。盻の場合、→∞とすれば完全定距離発見則となる。(式蘯のように考える。)2.1.3 逆3乗発見則目視の探知モデルは「逆3乗発見則」で表現可能であると言われている。これは、瞬間探知確率は目標物の大きさ(目標物がセンサーに対して張る立体角)に比例するという考え方である。逆3乗発見則は図1の距離-瞬間探知確率曲線のI型及びIII型を近似する。図2のように面積の目標物を高度から見下ろしている場合、面積の視線に垂直な投影面積はしたがって、目標物がセンサーに対して張る立体角は、として相対距離よりのとき図1 距離─探知確率センサー目標物図2 逆3乗発見法則の説明MSS技報・Vol.17 26瞬間探知確率は目標物の張る立体角に比例すると仮定すると、比例定数をとしてとおくと眈は目標物及び環境条件によって定まるパラメーターである。2.1.4 逆乗発見則瞬間探知確率が距離の単調減少関数で、至近距離の探知が確実な瞬間探知確率は眇でモデル化できる。2つのパラメーター( , )は、センサーの種別、目標物、環境条件などによって決まる。眇でとおくと、逆3乗発見則になる。また、の極限ではこれにを乗じると、に対してなので、連続センサーの完全定距離発見則盪になる。したがって、逆乗発見則は、特殊なケースとして逆3乗発見則と定距離発見則を含む一般的な法則と考えることができる。2.2 探知確率と探知ポテンシャル座標原点がセンサーに固定された「センサー座標系」からみた目標物の運動を考える(図3)。相対経路上を目標が相対速度で運動している。時刻における目標物の位置ベクトルをとする。距離にある目標を時間の間スキャンしたとする。時間的に重ならない探知が互いに独立と仮定すると、時刻までに目標を探知しない確率は以下をみたす。ここで、はの捜索で目標を探知しない確率で、瞬間探知確率をとすると、である。したがってとすると初期条件(最初は目標を0%しか探知できない)のもとに解くとしたがって、時刻0から時刻までに目標を発見する探知確率は眄ここで、時刻0から時刻に至る経路の探知ポテンシャル眩を導入すると、探知確率眄は眤これより、探知ポテンシャルが増大すると、探知確率は1に近づくことがわかる。また、第2.1節で述べた瞬間探知確率の有限時間にわたる積分として探知ポテンシャルは定義される。[探知ポテンシャルの加法性]探知ポテンシャルは「重ね合わせ」が可能である。図4のように、相対経路を二つに分解してとすると、それぞれの経路における探知確率は以下のようになる。ここで、経路で目標を探知するということは、、の少なくともいずれかで探知することを意味するから、余事象についての確率を考えてが成り立つ。これを眤と比較すれば以下の関係(探知ポテンシャルの加法性)を得る。センサー図3 センサー座標系からみた目標の運動のときこの加法性は、経路に沿う探知ポテンシャルがとのセンサーの合成についても成り立つ(図4)。2.3 横距離探知確率と有効捜索幅2.3.1 横距離探知確率探知ポテンシャル眩は一般的な曲線経路について定義されている。現実問題では、センサーから見ると、目標物は長時間、直線運動をする場合が多い。そこで、相対経路を直線経路に限定してモデル化しても差し支えない場合がある。相対経路を直線経路に限定すれば、探知ポテンシャルはセンサーからの最接近距離(CPA距離,Closest Point of Approach)で表される。このCPA距離を「横距離」という。ここで、横距離を通る直線を考え無限遠から接近し無限遠に去っていく目標を考える(図5を参照)。この目標の探知確率を「横距離探知確率」といい、以下で定義する。眞ただし、眩より眞はセンサーから測って横距離の位置に置かれた無限長の直線経路上のどこかで目標を探知する確率を表す。また、眞の定義では、無限長の直線経路を考えている。有限の大きさの探知可能圏を考える場合は、探知可能圏内の直線経路で積分して探知ポテンシャルを算出すればよい(図7を参照)。2.3.2 有効捜索幅横距離の分布は目標物の分布を意味し、これは確率変数と考えることができる。このの分布が一様、すなわち目標が一様分布しているとき、横距離探知確率曲線の下の面積は眥である(図6)。ここで、これと等価な面積を持つ高さ1、幅の長方形を考えると、これは探知レンジの完全定距離発見則に従うセンサーの横距離探知確率を表している(式盪より、探知レンジ内にある経路上で横距離探知確率は1、それ以外では0)。したがって、面積は完全定距離センサーの探知レンジ幅を表す。すなわち、である。この意味でを「有効捜索幅」という。いま、静止目標が単位面積あたり密度で一様に分布しているとする。この空間を横距離探知確率のセンサーを用いて捜索速力で目標を捜索するものとする。十分長い時間の間に、横距離の区間27センサーセンサー1センサー2図4 探知ポテンシャルの加法性センサー探知圏横距離図5 横距離を通過する目標数はである。このうちが探知されるから、の全域で探知される目標数の期待値は以下のように表せる。つまり、一定の捜索速力で目標空間を1回捜索するとき、探知される目標数の期待値は、横距離探知確率曲線の形状に関係なく、有効捜索幅に比例する。すなわち、上述のような「区域捜索」では、センサーの探知能力を表す特徴量として、横距離探知確率の代わりに有効捜索幅を用いることができる。[計算例]探知ポテンシャルを具体的に評価して、探知確率を算出した例を示す。図7に示すような長方形(大きさ)の領域を考える。この領域に外部から進入する物体があるとする。このとき、この進入物体が探知される確率について考える。以下の条件で、センサーからのCPA距離の位置を通過する物体の横距離探知確率をモデル化する。蘆センサーの探知法則は逆3乗則に従う。蘆センサーは領域内の位置に設置されている。蘆センサーの探知レンジはである。蘆進入物体がに平行に速力で進入し、進路は変更しない。蘆進入物体の監視は、センサーに初探知されてから領域を離脱するまで(図7秬参照)、または探知レンジを離脱するまで(図7秡参照)行なう。蘆この監視時間に基づいて横距離探知確率を評価する。まず、センサーの探知法則は、眈より以下のように表される。眦MSS技報・Vol.17 281 等面積0図6 有効捜索幅と横距離探知率曲線の関係進入点離脱点センサー探知圏センサー探知圏(a) (b)00 0図7 センサー位置と捜索領域ここで、である。また、逆3乗発見則の係数はで表されることを用いた(3)。次に、眦を積分して探知ポテンシャルを求める。秬のときこのケースはセンサーの探知範囲が離脱点を越えて下方まで広がっている場合である(図7秬を参照)。これは以下のように評価される。(i) のときとおくと眛ここで、のとき、となる。(ii) のときなのでだだし、で進入物体はセンサーの位置に到達することを考慮して、積分区間はとしている。とおくと眷これは、(i)の結果において、としたものに一致する。秡のときこのケースはセンサーの探知範囲が離脱点を越えない場合である(図7秡を参照)。積分範囲はとなるので秬の評価と同様にして(i) のとき眸(ii) のとき29ケース1ケース2 ケース38050進入経路S1 S3S201040センサー配置S1:(15, 10)S2:(40, 40)S3:(65, 10)センサー配置S1:(10, 10)S2:(40, 40)S3:(70, 10)センサー配置S1:(20, 10)S2:(40, 40)S3:(60, 10)図8 数値計算例睇探知ポテンシャル眛、眷、眸、及び睇を用いると横距離探知確率は睚で算出できる。進入物体が探知される確率を睚に基づいて調べてみる。領域の大きさをa=80km、b=50kmとする。探知レンジ=20kmのセンサー3個(S1,S2,S3)を以下のように領域に設置する(図8参照)。ケース1 S1:(20,10) S2:(40,40) S3:(60,10)ケース2 S1:(15,10) S2:(40,40) S3:(65,10)ケース3 S1:(10,10) S2:(40,40) S3:(70,10)ケース1と3は、センサーの探知範囲が離脱点を越えている場合で、探知ポテンシャルは眛と眷で算出される。他方、ケース2は、センサーの探知範囲が離脱点を越えない場合で、探知ポテンシャルは眸と睇による。このときの探知確率睚を示したものが、図8のケース1から3である。ケース1の横方向のセンサー配置では10< <70では高い確率で探知されるが、その外側では探知確率は急激に下がる。したがって、物体が領域の両端付近から進入すれば、センサーに探知されずに通過できる可能性が高くなる。ケース2と3は、センサーS1とS3を領域の外側にずらした場合である。ケース2では、どのような位置で物体が進入しても、およそ70%以上の確率で探知される。ケース3では、どのような位置でも90%以上の確率となる。だだし、ケース2と比較して=25km及び55km付近の確率が少し下がる。3.捜索システムとしての探知能力これまではセンサーの探知能力について述べてきた。しかし、通常の捜索は、航空機で海域を捜索する場合のように、センサーを搭載したビークル(航空機や船舶のような移動可能物体)を用いて行なわれることが多い。ここでは、センサーとビークルより成る捜索システムの能力について述べる。3.1 有効捜索率センサーを搭載したビークルが、単位時間に掃引する捜索面積の期待値を「有効捜索率」と定義する。この定義より明らかなように、有効捜索率は、「確率」ではなく、「時間率(rate)」の意味であり、[面積/時間]のディメンジョンをもつ量である。有効捜索幅のセンサーを用いて捜索速力で捜索したときの有効捜索率はで与えられる(図9参照)。3.2 カバレッジファクター有効捜索率は、捜索ビークルの単位時間当たりの捜索能力を表す特性値であるが、有効捜索率のビークルが時間捜索した場合、捜索領域をどの程度捜索したか(捜索の割合)を表す量として、「カバレッジ・ファクター(coverage factor)」CFがある。有効捜索率のビークルが、面積の領域を、時間捜索したときのカバレッジファクターは睨である(図9参照)。3.3 区域捜索の探知確率モデル有効捜索幅、有効捜索率、及びカバレッジファクターを用いる具体例として、区域をランダム捜索するモデルについて考える。静止目標が領域(面積)に存在する確率は一様分布に従うものとする。捜索者は有効捜索幅、捜索速度でランダム捜索を時間実施するとする(図10)。このとき、眤の導出と同様にして、時刻までの目標の未発見確率をとすればが成り立つ。これよりを得る。初期条件のもとに解けば、捜索時間の目標探知確率はMSS技報・Vol.17 30時間捜索のカバレッジファクター:有効捜索率(捜索面積/単位時間):捜索領域図9 有効捜索幅とカバレッジファクター睫となる。ただし、睨の関係を用いた。睫より、センサーの有効捜索幅が大きくなるほど、また捜索時間が長くなるほど、カバレッジ・ファクターCFが大きくなり、目標が探知される確率は1に近づくことが分かる。4.むすび目標物を探す場合の捜索理論の基礎概念について概観した。本稿では、探知確率の考え方(瞬間探知確率、探知ポテンシャル、探知確率)と捜索システムの能力(有効捜索率、カバレッジファクター)を中心として述べてきた。また、内容を連続センサーについて限定し、離散センサーについては言及しなかった。探知確率に関する事項の詳細については、飯田・宝崎の教科書(3)を参考にされたい。物探しは日常生活で頻繁に遭遇する。その場合、捜索理論を適用すれば効率的な物探しができる可能性がある。今後、捜索理論が一般の分野に広まり応用されることが期待される。参考文献盧飯田耕司:情報化時代の戦闘の科学―軍事OR入門,三恵社,190 pp.,2004.盪Koopman,B.O.:Search and Screening,OEGRep. No.56,172 pp.,1946.(2nd Ed.,PergamonPress,NY,1980.)蘯飯田耕司、宝崎隆祐:改訂捜索理論―捜索オペレーションの数理,三恵社,450 pp.,2003.31捜索領域捜索速力有効捜索幅目標の存在確率は一様分布図10 ランダム捜索