ステップストレス試験結果に基づく加速モデルの選択

ステップストレス試験結果に基づく加速モデルの選択
１．まえがき
電子機器に搭載される電子部品が、ユーザの満足が得られる耐用寿命（注1）を有しているかどうかを、開発工期の中で調べる必要がある。そのため、実際の使用条件（環境条件や作動条件の組合せ）よりも強いストレスを印加して、市場の使用期間よりも短期間で寿命のばらつき（寿命分布）を調べる加速寿命試験を実施する。試験条件における寿命分布から実使用における寿命分布を推定するには、ストレスの強さと寿命分布を関数で関連付ける加速モデルが必要になる。加速モデルは、3通り以上の条件に場合分けした加速寿命試験を繰り返し、それぞれの試験で得られた同じ累積故障確率（注1）に至るまでの試験時間と、ストレス強度の関係を関数化する手順で、試験結果から導き出される。最近の電子部品は、印加可能なストレス範囲が低下して、極端なストレスを印加できなくなり、故障が顕在化するまでの試験時間が長くなっている。このため、電子部品を使用する立場の機器メーカで、開発工期の中で3通り以上の条件の試験を繰り返すことができなくなり、加速モデルを調べることが困難になっている。このような背景もあり、信頼性試験の目的が、市場の寿命を予測することよりも、試験条件と合否の判断基準を定めた公的な試験規格に適合していることの検査へと変わってきた。そして、故障が顕在化する前に、規定の時間で試験が打ち切られ、寿命を予測したり、加速モデルを検証したりすることなく市場投入される事例も見られるようになってきている。
２．ステップストレス試験の導入
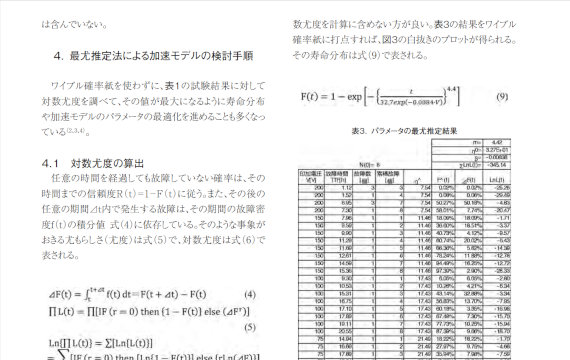
一方、使用用途や使用環境、関連した作動条件が多様化し、用途ごとの品質保証が必要になってきた。このため、限られた試験条件で確認した耐用寿命から、想定される市場の使用用途に応じた耐用寿命を予測することも必要になっている。また、安全上の配慮から、故障が発生した後の挙動を調べる目的で、故障が顕在化するまで試験を継続する必要もでてきている。これらの課題を解決するために、故障原因から実際に故障が現れるまでの因果関係（故障メカニズム）を変えずに、効率よく故障を顕在化させることができるステップストレス試験が適用されている。ステップストレス試験では、試験時間の開始後、印加するストレスを段階的に強めることで試験の加速性（加速係数）も段階的に高め、一定条件の加速寿命試験を継続するよりも、比較的短期間で、同じメカニズムの故障を顕在化できるようになる。ステップストレス試験は、ストレスが段階的に強まる試験であることから、試験開始から終了までの一連の試験の中で、いくつかの異なる条件の試験を実現していると捉えることができる。このことから、試験結果の解析方法を工夫すれば、加速モデルを調べることができるのではないかと考えられた。そこで、いくつかのステップストレス試験結果から加速モデルを検討したところ、従来の一定条件の加速寿命試験を3条件繰り返して得られる加速モデルと、比較的一致している加速モデルを得ることができた。以下にその内容をまとめる。第3章において、従来の加速モデルの検討手順を紹介する。第4章では、試験結果から最尤法を使った加速モデルの検討手順を示す。そして第5章で、ステップストレス試験から加速モデルが検討できることの検証結果を示し、第6章において、実際にステップストレス試験から加速モデルを検討した事例を紹介する。３．従来の加速モデルの検討手順表１は、元三菱電機㈱福山製作所の芝野氏から報告ステップストレス試験結果に基づく加速モデルの選択姫路事業所　技術第1部　技術第3課松岡　敏成、 井上　善裕（注1） 耐用寿命、耐用年数 t USE使用者が期待する使用期間を考慮して、設計段階から作りこむべき寿命。ある時間tを稼働した時点でも稼働を継続している台数をN(t)として、全出荷台数 N(0) に対する全故障台数{N(0)－N(t)}の割合F(t)を累積故障確率と呼ぶ。F(t)＝{N(0)－N(t)}／N(0)F(t)が社会的にも許容される範囲(業界ごとに異なる)の寿命を耐用寿命(または有用寿命)や耐用年数とすることが多い。58ステップストレス試験結果に基づく加速モデルの選択一般論文された（1）セラミックコンデンサのHAST（Highly Acceleratedhumidity and temperature Stress Test）による寿命分布を調べた結果である。通常の信頼性試験では印加しないであろう素子の限界ギリギリの高い電圧を印加することで、比較的短時間で故障の発生を確認している。表１．セラミックコンデンサのHAST試験結果表1の結果をワイブル確率紙（注2）に打点すると、図１のプロットが得られる。図１．セラミックコンデンサ寿命分布の電圧依存性図１のプロットにおいて、VB=200［V］とVB=100［V］の打点の中に、他の打点に比べて故障までの時間が短い打点が観られるが（破線の囲み内）、これは試験電圧が過大となり、瞬間的な過電圧破壊が発生したデータが含まれたためであると考えられる（故障原因と故障現象が他の試料と異なる）。この分析結果から、セラミックコンデンサの寿命分布は、式（1）、式（2）で近似できる。表２は、式（1）、式（2）と図１の近似式から導かれる特性寿命η（注2）を比較した結果である。表２．電極電圧と特性寿命の関係表２の結果から図２が得られる。図２．特性寿命と試験電圧の関係今回の試験に適用されたセラミックコンデンサの寿命分布は、式（3）で推定することができる。式（3）においては、試験温度や湿度に関して条件の場合分けを行っていないので、印加電圧以外の因子の影響（注2） ワイブル分布関数 F(t)＝1-exp[-{(t/η)m}]の両辺の二度対数をとれば、式（1）のようなLn(t)の一次式に変形できる。横軸がLn(t)、縦軸がLnLn[1/{1-F(t)}]となるように、tとF(t)の値で打点できる確率紙。ηはF(t)=1-exp(-1)になる特性寿命を表す尺度パラメータ、mはプロットの傾きで分布の形を表す形状パラメータ。1より大きい摩耗故障、ちょうど１の偶発故障、1より小さい初期故障を識別できる。59ステップストレス試験結果に基づく加速モデルの選択は含んでいない。４．最尤推定法による加速モデルの検討手順ワイブル確率紙を使わずに、表１の試験結果に対して対数尤度を調べて、その値が最大になるように寿命分布や加速モデルのパラメータの最適化を進めることも多くなっている（2、3、4）。４．１　対数尤度の算出任意の時間を経過しても故障していない確率は、その時間までの信頼度R（t）=1－F（t）に従う。また、その後の任意の期間⊿t内で発生する故障は、その期間の故障密度（f t）の積分値 式（4）に依存している。そのような事象がおきる尤もらしさ（尤度）は式（5）で、対数尤度は式（6）で表される。４．２　加速モデルの検討ワイブル確率紙を使った寿命分布の検討結果も参考に、寿命分布として式（7）で表されるワイブル分布を仮定し、加速モデルとして特性寿命が式（8）で表される指数関数モデルを仮定して、それぞれのパラメータm（形状パラメータ）、η（尺度パラメータ、特性寿命）、β（試験結果から得られる印加電圧の比例定数）を最適化することを検討する。表３は、ExcelのSOLVER機能を使って、m、η0、βに仮の値を設定して対数尤度Σ{LnL（t）}を算出し、その値が最大になるように、それぞれのパラメータを調整して得られる、寿命分布と加速モデルの関係を調べた結果である。この時、過電圧破壊（故障メカニズムが異なる）データの対数尤度を計算に含めない方が良い。表３の結果をワイブル確率紙に打点すれば、図３の白抜きのプロットが得られる。その寿命分布は式（9）で表される。表３．パラメータの最尤推定結果図３．最尤法による寿命分布モデルの最適化５．ステップストレス試験試験の開始から、試験時間の一定のインターバルタイムtiを経過するごとに、印加するストレスの強さを一定量⊿Vずつ強めていくステップストレス試験を適用すれば、一定の強さのストレスを印加し続ける加速寿命試験よりも、短時間で故障を顕在化させることができる。ただし、試験時間の60ステップストレス試験結果に基づく加速モデルの選択短い領域と長い領域で加速係数αiが異なるので、それぞれのインターバルタイムごとにαiを導き出し、想定する実使用条件における動作時間に換算して、その累積和から実使用における寿命分布を調べる必要がある。この試験条件と実使用時の寿命換算の関係を、図４と図５で示している（5）。図４．ステップストレス試験の進め方図５．ステップストレス試験結果の実動作換算表３の結果に対して、スタート電圧V0＝25［V］、ステップ電圧⊿V=25［V］、インターバルタイムti=3［h］の条件で、ステップストレス試験を実行した場合の試験結果は、式（9）のモデルを適用して換算することで、表４のような試験結果が得られると推定できる。表４のNsは試験完了ステップサイクル数、tfはステップストレス試験における故障までの時間、tendは最終ステップにおける故障までの時間である。実際に表４のような試験結果が得られたと仮定して、仮の加速モデルと寿命分布を適用し、対数尤度Σ{LnL（t）}を調べ、Σ{LnL（t）}が最大になるパラメータを見つけ出すと、表５の結果が得られる。表５のt2［5 h］は、表４のステップストレスに対して、通電電圧VB=25［V］一定とした場合の表４のtfの換算時間である。iはt25を昇順に並べたときの順序を表している。F^は、各t 25における累積故障確率の推定値F（t25）。jはF^を昇順に並べ替えるための番号で、Fj^はF（t25）を昇順に並べ変えた値となっている。rjはj番目のデータの故障数、⊿FはFj+1^－Fj^で算出できる。J番目のデータが現れる尤度Ljは、rjが0ならば 1－Fj^で表され、rjが0でないならば （⊿F）rで表される。加速モデルは通電電圧VBに依存する特性寿命ηに対するパラメータβを含む指数関数モデルで、寿命分布は形状パラメータmを含むワイブル分布で表されることを仮定してパラメータの調整を行っている。表４．表３から推定したステップストレス試験結果表５．ステップストレス試験に基づく加速モデル表５の結果から、印加電圧V［V］における寿命分布は、式（10）として得られる。61ステップストレス試験結果に基づく加速モデルの選択表６．試験電圧ごとの寿命分布の推定値図６．ステップストレス試験結果式（10）で得られた試験電圧と寿命分布の関係から、表３の試験電圧200［V］、150［V］、100［V］、75［V］で得られたF（t）に相当する故障までの時間t^を調べると表６の結果が得られる。t^は式（11）に従って算出している。もし、今回検討しているステップストレス試験結果から加速モデルを検討する手順が妥当であれば、表６の結果と表３の結果はほぼ一致しているはずである。図６は図３に表６の結果を重ねてそのことを確認したもので、図１の試験結果や図３の推定モデルにも比較的一致したプロットが得られることが確認できる。６．パワーデバイスの電圧加速モデルパワーデバイスの高電圧スクリーニング（注3）を適用する際に、実使用の何年相当のストレスが印加されているかを検討するために、印加電圧と印加時間に対してステップストレス試験を実施し、印加電圧の寿命分布に対する加速モデルを検討した。スタート電圧45［V］から55［V］までは5［V］ステップで、55［V］以上は1［V］ステップで通電電圧を段階的に高め、電源端子やI/O端子の電気的特性を測定して故障判定を行っている。表７がステップストレス試験結果である。表７．パワーデバイスの高電圧試験結果表７の結果に対して加速モデルとしてηに式（13）のモデルを仮定し、パラメータのη0とβを、対数尤度が最大になるように調整した結果が表８と表９である。通電電圧が実動作電圧で一定であることを想定した場合の故障までの時間に換算している。（注3） IC素子内部のゲート酸化膜や配線層間の絶縁膜に実使用よりも大きめの電圧ストレスを印加して、製造欠陥などにより絶縁強度が低下した初期故障品を、出荷前に取り除くための処置。時間依存性のある酸化膜破壊などの故障メカニズムに特化することになるが、完成品バーンインよりも、短時間で効率よく初期故障を検出することができる。62ステップストレス試験結果に基づく加速モデルの選択表８．高電圧試験結果の実動作寿命換算表９．高電圧試験のパラメータ推定結果表９の結果から、この高電圧試験の加速モデルとして、式（14）が得られた。表８の加速係数が非常に大きな値になっている。この式（14）のモデルが適切なのか疑われるところであるが、別ロットで実施したステップストレス試験結果を同様に解析して得られたβの値が0.758であったことからも、決して大きく的を外した解析結果とは言えないと考えている。７．むすび従来、故障を顕在化させることも困難であった一定条件の信頼性試験に対して、ステップストレス試験を適用することで、比較的短時間で同じモードの故障を顕在化させることができるようになる。故障が顕在化して故障データが得られることで、ストレスのステップアップの仕方やインターバル時間のとり方も考慮して、加速モデルを調べることもできた。加速モデルが得られれば、試験結果から各使用環境ごとの寿命推定も可能になる。加速モデルを検討するために、尤度の大きさを比較する最尤法で、最適なモデルであることを数値的に判断できるようになる。また、既知のモデルに従うことが自明で、そのモデルに含まれるパラメータを推定する場合でも、一組のステップストレス試験結果が採取できればよいので、大幅な試験効率の改善が期待できる。ただし、過剰なストレスとなって、故障メカニズムの異なる故障データが混在することで、推定値を誤ることにつながる。故障品の物理解析を通して、同じ故障メカニズムであることを確認しておくことも必要になる。参考文献（1） 芝野照夫“, チップ型セラミックコンデンサの耐湿性能の実力値評価”,第44回信頼性保全性シンポジウム,Session1–2（ 2014）（2） 貝瀬徹“, 確率過程モデルに基づく劣化データの信頼性解析”,電子情報通信学会技術研究報告,IEICETechnical Report,21～24（ 2010）（3） 松岡敏成“, 最尤推定法に基づくセラミックコンデンサの電圧加速モデルの選択”,電子情報通信学会技術研究報告,IEICE Technical Report,pp.7～14（2014）（4） 松岡敏成“, 最尤推定法を使った製造条件範囲の最適化”,電子情報通信学会技術研究報告,IEICETechnical Report（ 2016）（5） Luis A. Escobar and William Q. Meeker“, AReview of Accelerated Test Models, StatisticalScience”,Vol. 21, No. 4, 552～577（ 2006）執筆者紹介松岡　敏成 マツオカ　トシナリ1985年入社。主に品質管理や信頼性管理のための統計的データ解析の応用技術開発に従事。現在、姫路事業所技術第1部技術第3課。井上　善裕 イノウエ　ヨシヒロ1992年入社。主に半導体デバイスの信頼性試験技術開発に従事。現在、姫路事業所技術第1部技術第3課。63ステップストレス試験結果に基づく加速モデルの選択