時系列データに対する異常検知のための教師なし学習方法の提案

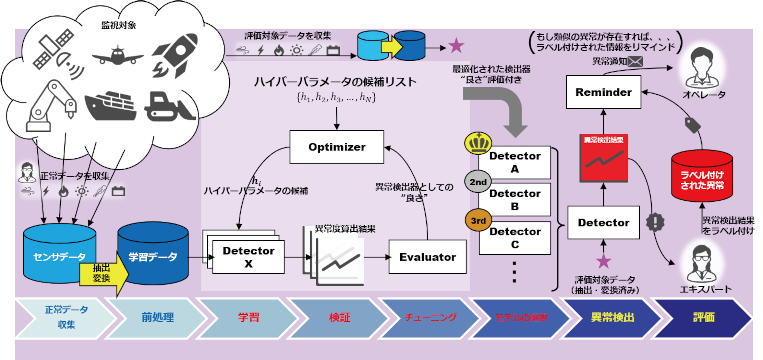
1 MSS 技報・Vol.31
時系列データに対する異常検知のための教師なし学習方法の提案
A proposal for unsupervised learning method for time series anomaly detection
太田 聡＊Satoshi Ota
時系列データを対象とした異常検知を行う際に、異常データの事前情報が収集困難な場合や、未知の異常検知を目的として、教師なし学習による異常検知を行う場合でも、教師なし異常検知モデルに依存しない定量的な性能評価が可能となる手法を検討した。これにより、教師なし異常検知モデルのハイパーパラメータの最適化や異常判定のための閾値の設定が容易になることが期待できる。本報では、この手法について紹介するとともに、この手法を使って実際に試行した異常検知結果を示す。
In this paper, we propose an unsupervised learning method for time series anomaly detection,which is independent of unsupervised anomaly detection models. Although unsupervised anomalydetection is effective when it is difficult to collect anomaly data beforehand or when the goal is todetect unknown anomalies, there is a problem that there is no model–independent performance metricssuch as the normal/abnormal sample accuracy in supervised learning. We use Kullback–Leiblerdivergence between the predictive distribution of time–series anomaly scores based on Gaussianprocess regression and the actual distribution of calculated anomaly scores as a metrics for evaluatingthe performance of anomaly detectors using unsupervised learning. This method is expected tofacilitate the optimization of hyperparameters for unsupervised anomaly detection models and thesetting of thresholds for anomaly score. In this paper, we introduce the proposed method and showthe actual anomaly detection results of the proposed method.
＊つくば事業部 第一技術部
1．まえがき
近年では、情報通信技術の発展によりセンサデータの収集が容易になり、時系列データから機械学習によって異常状態を検知する技術の利用が活発化している。データに基づく客観的な基準で問題の兆候を捉え、いち早く意思決定を行うことは、コストを最小化し、安全を確保する意味で重要である。システムが複雑化し、人的資源も限られている状況からも、これを自動検知する技術を確立することは社会的な要請と言える。著者が所属している三菱スペース・ソフトウエア株式会社つくば事業部第一技術部では、ロケットの航法誘導ソフトウェアの開発や宇宙機運用支援業務等で培った宇宙関連のドメイン知識を有している。そのような我々が異常検知をはじめとする機械学習の関連技術により更なる価値を提供することは、宇宙開発の発展に寄与するものとの考えのもと、機械学習関連技術の獲得、及び新規技術開発に取り組んでいる。本報では、その一例として、時系列データを対象とした異常検知技術について紹介する。時系列データから異常検知を行う場合、異常データに関する事前情報（教師データ）が収集困難であることが実用上の問題になるケースが多い。また、異常データの事前情報を基に学習したモデルを用いる場合でも、未知の異常への対応が課題となる。このような場合、正常なデータから正常状態を表すモデルを学習した異常検出器を構築し、正常状態からの逸脱を異常スコアとして算出する教師なし学習が有効である。一方で、教師なし学習による異常検知では教師あり学習における正常・異常標本精度のような直接的な異常検出性能を評価する指標がないという実用上の問題がある。そのため、学習モデルのハイパーパラメータのチューニングや異常判定のための閾値の設定が課題となる。本報では、教師なし学習で生成した異常検出器に2 MSS 技報・Vol.31よって算出された時系列の異常スコアを確率過程回帰によって予測した際の尤もらしさ（予測誤差分布と実際に算出された異常スコアの分布のKullback–Leibler ダイバージェンス）を異常検出器の性能評価指標として導入する。これにより、ハイパーパラメータの探索、及び異常判定の閾値の自動化を図る手法を提案する。この評価指標は異常検知手法に依存しないため、異なる異常検知手法に対して同様に適用可能である。最後に、提案手法を用いて宇宙機のテレメトリデータから異常予兆を検出した試行結果を示す。2．提案手法の位置づけ提案手法について述べる前に、実際に機械学習を応用した異常検知システムを構築することを想定して描いた全体像（以下、提案システム）を図１に示す。機械学習を実際の問題に適用する際、はじめから汎化能力の高い異常検出器が構築できないのが通常である。汎化能力の高い異常検出器を得るためには、ドメイン知識を基礎とした収集データの理解をはじめとして、問題解決に適用可能な異常検知手法の検討、異常検知手法によるモデルの学習、学習済みモデル（異常検出器）を用いた検証、検証結果に基づくモデルのチューニングや異常判定閾値の設定といった手続きが必要になる。加えて、ノーフリーランチ定理として知られるように、どのような問題に対しても万能な異常検知手法は存在しないため、学習済みモデルの検証ではモデルに依存しない定量的な評価指標によって評価したい。提案システムでは、そのような評価器（Evaluator）を導入することで学習からハイパーパラメータの最適化を含むモデルの選択と異常判定閾値の設定までの自動化を狙っている。本報では、提案システムへの適用を目的とした異常検出手法（Detector）、異常検出器の評価手法（Evaluator）、異常検出手法のハイパーパラメータの最適化手法（Optimizer）、及び構築した異常検出器の算出した異常スコアから対象システムの異常状態を判定する異常判定手法（Reminder）の概要について述べる。ここで、実際のシステム構築では外部（監視対象）から各種センサデータを取得・抽出し、機械学習処理に入力可能なデータ形式に加工するなどの前処理技術や構築した異常検出器の運用成果を基にした異常検知システムの評価も重要な要素であるが、ドメイン依存の高い課題であるため、以下の記述では割愛する。3．提案手法本章では前章で示した提案システムを構成する各手法の概要について述べる。なお、以下の手法の検討においては、参考文献⑴ ⑵ ⑶を参考にしている。また、以下では監視対象とするシステムから収集されるマルチセンサデータを𝑀𝑀𝑀𝑀 次元ベクトル𝒙𝒙𝒙𝒙 、時系列のセンサデータの集合を𝒟𝒟𝒟𝒟 と表記する。また、平均𝝁𝝁𝝁𝝁 、共分散行列𝚺𝚺𝚺𝚺 の正規分布を𝒩𝒩𝒩𝒩(𝒙𝒙𝒙𝒙|𝝁𝝁𝝁𝝁, Σ) と表記する。3.1　異常検知手法提案システムでは異なる複数の異常検知手法を評価することを想定していることから、図２に示すように異常検出器の仕様を統一する。各異常検出器は、ある時刻を図１　時系列データからの異常検知システムのイメージ3 MSS 技報・Vol.31特徴付ける多次元時系列データのサブセットと当該手法のハイパーパラメータを入力として、任意の時刻の異常スコアを算出するよう設計する。また、異常検出手法が学習により異常検出器を生成（各手法の未知のパラメータを推定）する際に入力される学習データ（多次元時系列データのサブセット）は正常データであり、異常検出器が出力する異常スコアは正常状態からの逸脱を反映したものであることを前提とする。すなわち、教師なし学習による異常検知手法を適用するため、異常データに関する事前情報（教師データ）を必要としないこととする。3.2　異常検出器の評価手法前節に示した各異常検出器が算出した時系列の異常スコアを用いて異常検出器の性能を評価する。ここで、対象とする異常スコアは正常データを用いて算出されたものとし、定性的に妥当な異常検出器であれは正常データから算出される異常スコアは定常的なもの、あるいは経年劣化等によるシステムの状態変化を反映したものであっても評価区間のタイムスケールでは定常的と仮定する。リアルタイムの時系列データに対する異常検知では過去のデータでしか学習できないため、算出される異常スコアがそのような性質を持つことが望ましい。このような異常スコアの変動であれば、過去の時系列異常スコアの回帰分析の結果として未来の異常スコアを予測した場合でも妥当な結果が期待でき、異常スコアの逸脱の判定が容易である。提案手法では異常スコアの回帰モデルとして推定の不確実性も表現可能なガウス過程回帰を導入し、ガウス過程回帰による異常スコアの予測結果と実際に算出された異常スコアを比較し、その予測の尤もらしさを異常検出器の性能として評価する。この異常検出器の評価手法の手続きの概略を図３に示す。各ステップの概要は次のとおり。Step ０：ハイパーパラメータℎ を用いた異常検知手法の異常検出器を評価するためのデータとして、正常データのみ含まれるデータを用意し、訓練データと検証データに分割する。ここで、訓練データには正常データのうち、過去側のデータを、検証データには同じく未来側のデータをそれぞれ使用する。Step １：訓練データにより正常モデルを学習し、異常検出器を生成（異常検知手法の未知のパラメータを学習）する。Step ２：生成した異常検出器を用いて、訓練データ（過去）と検証データ（未来）における異常スコアを算出する。Step ３：算出した異常スコアの時系列をガウス過程回帰によって推定し、その予測結果と検証データ（未来）における異常スコアを比較して、異常検出器の尤もらしさを評価する。ここで、Step ３での尤もらしさの評価では、時々刻々の異常スコア𝑎𝑎𝑎𝑎𝑖𝑖𝑖𝑖 をガウス過程回帰で推定した異常スコアの期待値𝑎𝑎𝑎𝑎𝑖𝑖𝑖𝑖 と分散𝜎𝜎𝜎𝜎𝑖𝑖𝑖𝑖 を用いて次式のとおり標準化する。𝑎𝑎𝑎𝑎𝑖𝑖𝑖𝑖 ↦ 𝑎𝑎𝑎𝑎′𝑖𝑖𝑖𝑖 = ⑴𝑎𝑎𝑎𝑎𝑖𝑖𝑖𝑖 − 𝑎𝑎𝑎𝑎𝑖𝑖𝑖𝑖𝜎𝜎𝜎𝜎𝑖𝑖𝑖𝑖このような標準化を行うことで、標準化異常スコアの期待される確率分布𝑝𝑝𝑝𝑝(𝑎𝑎𝑎𝑎′) = 𝒩𝒩𝒩𝒩(𝑎𝑎𝑎𝑎′|0,1) と実際に標準化異常スコアから経験的に求めた標準化異常スコア確率図２　異常検知手法の概要図３　異常検出器の評価手法の概略4 MSS 技報・Vol.31分布𝑞𝑞𝑞𝑞(𝑎𝑎𝑎𝑎′) の確率分布間の相違度を次式に示すKullback–Leibler ダイバージェンスとして定量的に算出できる。𝐾𝐾𝐾𝐾𝐾𝐾𝐾𝐾(𝑝𝑝𝑝𝑝||𝑞𝑞𝑞𝑞) = 􀶱𝑝𝑝𝑝𝑝(𝑎𝑎𝑎𝑎′) ln ⑵𝑝𝑝𝑝𝑝(𝑎𝑎𝑎𝑎′)𝑞𝑞𝑞𝑞(𝑎𝑎𝑎𝑎′)𝑑𝑑𝑑𝑑𝑎𝑎𝑎𝑎′Kullback–Leibler ダイバージェンスは確率分布間の距離に相当する尺度で、これが０に近いとき、望ましい異常スコアが算出可能な異常検出器であると判断する。なお、このような評価手法において注意すべきは、入力されるセンサデータに関係なく単に定常的な異常スコアを出力する異常検出器も望ましいものとして判断されてしまう点である。このような異常検出器を選択してしまうことを避けるために、採用する異常検出手法を選択する段階で、適用する問題に対して定性的に妥当な手法であるかを検討するとともに、正常データを加工して人工的に生成した異常データに対する感度を評価する等の対処が必要になる。3.3　異常検出器の最適化手法前節の異常検出器の評価指標に基づいて、異常検知手法の最適なハイパーパラメータを探索する。探索手法は任意の手法が適用可能である。代表的な探索手法として以下の手法があげられる。グリッドサーチ：指定されたハイパーパラメータの候補値の全ての組み合わせを全て試す。ランダムサーチ：指定されたハイパーパラメータの範囲から、ランダムに候補値をサンプリングして探索する。ベイズ最適化：ハイパーパラメータに対する異常検出器の指標の分布がガウス過程に従うとして、指標値の分布を逐次推定しながら重要な候補値を選択して探索する。3.4　異常判定手法前節までの手続きによって構築された異常検出器を用いて、時々刻々入力されるセンサデータに対して異常スコアを算出し、監視対象とするシステムの正常状態からの変化度（異常状態への遷移）を監視する。変化度は異常検出器が過去データに対して算出した異常スコアのガウス過程回帰による予測値を用いた累積和として算出する。累積和の算出イメージを図４に示す。図４では、ある時刻における異常スコアの確率分布（青）と状態の遷移に対応する異常スコアの分布上振れ（黄：＋３𝜎𝜎𝜎𝜎 ）、下振れ状態（橙：－３𝜎𝜎𝜎𝜎 ）を示しており、累積和はこのような上振れ状態への状態変化を示す上方累積和𝑈𝑈𝑈𝑈𝑖𝑖𝑖𝑖 と、下振れの状態への状態変化を示す下方累積和𝐿𝐿𝐿𝐿𝑖𝑖𝑖𝑖 として次式によって算出される。𝑈𝑈𝑈𝑈𝑖𝑖𝑖𝑖 = 􁉐 ⑶0, 𝑖𝑖𝑖𝑖 = 0max 􁉆0, 𝑈𝑈𝑈𝑈𝑖𝑖𝑖𝑖−1 + ln𝒩𝒩𝒩𝒩(𝑎𝑎𝑎𝑎𝑖𝑖𝑖𝑖|𝑎𝑎𝑎𝑎𝑖𝑖𝑖𝑖 + 3𝜎𝜎𝜎𝜎𝑖𝑖𝑖𝑖, 𝜎𝜎𝜎𝜎𝑖𝑖𝑖𝑖)𝒩𝒩𝒩𝒩(𝑎𝑎𝑎𝑎𝑖𝑖𝑖𝑖|𝑎𝑎𝑎𝑎𝑖𝑖𝑖𝑖, 𝜎𝜎𝜎𝜎𝑖𝑖𝑖𝑖)􁉇⑷ここで、上式の上振れ下振れ状態のオフセット値±3𝜎𝜎𝜎𝜎は異常判定手法のパラメータであり、任意の値が設定される。また、監視すべき状態変化は異常スコアの上振れであるため、上方累積和が主な監視対象となる。監視対象のシステムが異常状態に変化したとき、上方累積和は単調増加することになり、これが閾値を超えた段階で異常状態と判定する。累積和の閾値設定においては、学習に用いた過去データに対して算出した累積和の統計評価（最大値、パーセンタイル等）を基準とすることができる。例えば、パーセンタイルを用いて許容する誤報頻度から閾値を設定することも可能である。4．異常検知の試行本章では前章にて提案する手法を用いて異常検知システムを試作し、宇宙機の実データを用いて異常検知を試行した結果を示す。試行の対象とするデータには、先行研究⑷の存在するX 線天文衛星「すざく」の電源系機器のデータを用いた。当該研究によると、すざく衛星の打ち上げ７年目の2012 年１月24 日に電源系機器の異常が原因と考えられるSAFEHOLD（何らかの原因で異常が発生した場合、熱電気的に安全な姿勢を保持するモード）図４　累積和算出イメージ𝐿𝐿𝐿𝐿𝑖𝑖𝑖𝑖 = 􁉐0, 𝑖𝑖𝑖𝑖 = 0min 􁉆0, 𝐿𝐿𝐿𝐿𝑖𝑖𝑖𝑖−1 − ln𝒩𝒩𝒩𝒩(𝑎𝑎𝑎𝑎𝑖𝑖𝑖𝑖|𝑎𝑎𝑎𝑎𝑖𝑖𝑖𝑖 − 3𝜎𝜎𝜎𝜎𝑖𝑖𝑖𝑖, 𝜎𝜎𝜎𝜎𝑖𝑖𝑖𝑖)𝒩𝒩𝒩𝒩(𝑎𝑎𝑎𝑎𝑖𝑖𝑖𝑖|𝑎𝑎𝑎𝑎𝑖𝑖𝑖𝑖, 𝜎𝜎𝜎𝜎𝑖𝑖𝑖𝑖)􁉇5 MSS 技報・Vol.31が発生しており、本試行でも当該異常の予兆を検出することを目的とした。4.1　試行条件すざく衛星の電源系機器の異常（SAFEHOLD）が発生（2012–01–24 01:27:46）するまでの直近約１年間を異常検知の対象期間とした。学習に供するデータにはDARTS ⑸で公開されているすざく衛星のHK（Housekeeping）データから電源系機器の電圧・電流の７項目のデータ（図５）を抽出して利用した。異常検知手法には後述する疎構造学習法（4.1.1 項参照）を使用し、経年的なシステムの状態変化を考慮して、10 日ごとに学習モデルを更新した。学習データには40 日分のデータを30 日分の訓練データ（過去）と10 日分の検証データ（未来）に分割したデータを用いた。ハイパーパラメータは１日間隔で作成した過去10ケース分の学習データで算出した式⑵の指標の平均値を用いてベイズ推定法で探索した。また、異常判定に用いる上方累積和の閾値には最適化されたハイパーパラメータを適用した異常検出器を用いて異常検知の評価期間の開始時刻から過去30 日分の上方累積和を算出したときの最大値の３倍値を適用した。4.1.1　疎構造学習法本試行で適用した異常検知手法である疎構造学習法について概説する。本試行で用いる疎構造学習法は、具体的には確率分布𝑝𝑝𝑝𝑝(𝒙𝒙𝒙𝒙) として多変量正規分布を想定したマルコフグラフを推定するガウス型グラフィカルモデルと呼ばれるモデルである。次式は各センサデータ（ 𝒙𝒙𝒙𝒙 の各成分）を標準化後の多変量正規分布（標本平均𝟎𝟎𝟎𝟎 、各成分の分散１）を表す。なお、疎構造学習自体は多変量正規分布に限定されるわけではなく、その他の確率分布にも拡張可能である。𝒩𝒩𝒩𝒩(𝒙𝒙𝒙𝒙|𝟎𝟎𝟎𝟎,𝚲𝚲𝚲𝚲−1) = ⑸|𝚲𝚲𝚲𝚲|12(2𝜋𝜋𝜋𝜋)𝑀𝑀𝑀𝑀2exp 􀵜−12𝒙𝒙𝒙𝒙T𝚲𝚲𝚲𝚲𝒙𝒙𝒙𝒙􀵠ガウス型グラフィカルモデルにおける未知のパラメータはM × M 次元の精度行列Λ （共分散行列Σ の逆行列）である。疎構造学習ではより本質的な直接相関を反映した疎な精度行列をグラフィカルラッソ（graphical lasso）と呼ばれる手法を用いて正常データの標本𝒟𝒟𝒟𝒟normal から推定（学習）する。推定手法の詳細は割愛するが、疎構造学習法では疎な（より本質的な直接相関のみを反映した）精度行列を求めるため、精度行列の事前分布𝑝𝑝𝑝𝑝(Λ)として次式に示すラプラス分布を用いた最大事後確率推定により推定する。𝑝𝑝𝑝𝑝(𝚲𝚲𝚲𝚲) = ⑹𝜌𝜌𝜌𝜌2exp 􁉌−𝜌𝜌𝜌𝜌 􀷍 􀸫𝚲𝚲𝚲𝚲𝑖𝑖𝑖𝑖,𝑗𝑗𝑗𝑗􀸫𝑀𝑀𝑀𝑀𝑖𝑖𝑖𝑖,𝑗𝑗𝑗𝑗=1􁉍ここで、𝜌𝜌𝜌𝜌 > 0 は推定される精度行列の疎密性を制御するパラメータであり、その値が大きいほど精度行列はより疎になる。𝜌𝜌𝜌𝜌 は疎構造学習のハイパーパラメータであり、異常検知性能を最大化させるように決定する必要がある。疎構造学習により学習したモデル（精度行列）を用いた時刻𝑡𝑡𝑡𝑡 の異常スコアは次式のとおり変数（センサ）ごとに算出される。𝑎𝑎𝑎𝑎𝑖𝑖𝑖𝑖 = ⑺12ln𝚲𝚲𝚲𝚲𝑖𝑖𝑖𝑖,𝑖𝑖𝑖𝑖𝚲𝚲𝚲𝚲′𝑖𝑖𝑖𝑖,𝑖𝑖𝑖𝑖−12􁉊[𝚲𝚲𝚲𝚲𝚲𝚲𝚲𝚲𝚲𝚲𝚲𝚲]𝑖𝑖𝑖𝑖,𝑖𝑖𝑖𝑖𝚲𝚲𝚲𝚲𝑖𝑖𝑖𝑖,𝑖𝑖𝑖𝑖−[𝚲𝚲𝚲𝚲′𝚲𝚲𝚲𝚲𝚲𝚲𝚲𝚲′]𝑖𝑖𝑖𝑖,𝑖𝑖𝑖𝑖𝚲𝚲𝚲𝚲′𝑖𝑖𝑖𝑖,𝑖𝑖𝑖𝑖􁉋ここで、上式のΣ は学習に用いた正常データの標本𝒟𝒟𝒟𝒟normal から算出した標本共分散行列、Λ′ は時刻𝑡𝑡𝑡𝑡 を特徴づける時系列データの標本𝒟𝒟𝒟𝒟𝑡𝑡𝑡𝑡′ から推定した精度行列である。また、時系列データによる異常検知において正常データ𝒟𝒟𝒟𝒟normal の標本は異常検知の対象となる𝒟𝒟𝒟𝒟𝑡𝑡𝑡𝑡′ より過去に収集された標本である。4.2　試行結果実際にすざく衛星の電源系のデータを用いて異常検知を実施した結果を図６に示す。図６は異常が発生した時刻より約10 日以上過去のデータを使って学習したモデル（精度行列）を使って⑺式によって算出した時々刻々の各成分の異常スコアの絶対値を電源系システムの異常スコアとし、3.4 節に示す手続きによって累積和を評価した結果である。ここで、時々刻々の異常スコアを算出する際に異常検出器に入力する当該時刻を特徴づける標本には、すざく衛星の軌道周期を考慮して当該時刻の直近の96分の過去データを用いた。図６に示すとおり、提案する手法により、異常発生の約13時間前に異常を検出することに成功している。加えて、この時の異常検出器の図５　すざく衛星 電源系HK データ例当図はDARTS ⑸から取得したX 線天文衛星「すざく」のHK データから以下に示す7 項目の電圧・電流値を抽出、プロットしたものである。各データともX 線天文衛星「すざく」の軌道周期（約96分）と同期した変動を示している。（DIST_BATA_I_CAL/DIST_BATB_I_CAL/DIST_PCU_IN_I_CAL/DIST_PCU_OUT_I_CAL/DIST_BATA_V_CAL/DIST_BATB_V_CAL/DIST_PCU_BUS_VOL_CAL）6 MSS 技報・Vol.31学習結果を図７に示す。図７は疎構造学習によって学習された精度行列の０でない非対角成分を持つ要素同士に辺が存在する対マルコフグラフであり、各辺の数値は精度行列から算出した偏相関係数である。得られた対マルコフグラフとその偏相関係数から、電源系機器の冗長系の対照的な構造や、各センサデータのIN/OUT に対する正負の相関が妥当に反映されていることがわかる。この結果から、定性的にも妥当な異常検出器により異常が検出されていたことが確認できた。なお、今回のケースで同時に評価した異常発生イベントを含まない過去１年分の評価領域において異常判定となる誤報は発生しなかった。5．むすび本報では、時系列データを対象とする異常検知技術について紹介した。提案手法では、事前に異常データが入手困難である場合に、教師なし学習を異常検知手法として用いつつも、教師なし学習で算出される異常スコアの確率過程回帰の予測性の尤もらしさを異常検出器の評価基準として導入した。これにより、異なる異常検知手法の比較やチューニングを行うものである。また、提案手法の試行例としてX 線天文衛星「すざく」の電源系の異常予兆が検出できることを示した。一方で、当該試行の成功要因の一つとして、対象とした学習データが周期的なデータであることが挙げられる。その点で、試行例は比較的容易に異常検知可能な問題だったと考えられる。今後は更に実用的な課題に対応するため、モード変更が頻繁なデータ（複数の正常モード）への対処や、よりロバストな異常検出器構築のためのアンサンブルモデルの適用、データ理解に基づく異常状態に対する感度が高い疑似的なセンサ値の設定（例：冗長系のセンサ値の差分）等の改良を図っていく予定である。また、提案手法を含む異常検知技術を様々な課題に対して適用することで、持続可能な社会の実現、及び宇宙開発をはじめとする科学技術の発展に寄与していきたい。本報で紹介したX 線天文衛星「すざく」を対象とした異常検知の試行に利用したデータは、宇宙航空研究開発機構・宇宙科学研究所、科学衛星運用・データ利用ユニット（C–SODA） が運営するData ARchives andTransmission System（DARTS）から取得したものである。参考文献(1) 井手 剛：入門 機械学習による異常検知－ R による実践ガイド－，コロナ社（2015）図６　すざく衛星 電源系機器 異常発生時の累積和による異常検知結果図７　学習モデル（対マルコフグラフ）7 MSS 技報・Vol.31(2) 井手 剛，杉山 将：異常検知と変化検知，講談社（2015）(3) 持橋 大地，大羽 成征：ガウス過程と機械学習，講談社（2019）(4) 梅津 里香，杉江 卓哉，長瀬 雅之，湖海 亮，竹島 敏明，海老沢 研，満田 和久，山本 幸生：機械学習を用いた宇宙機の故障の予兆検知，宇宙航空研究開発機構研究開発報告：宇宙科学情報 解析論文誌：第８号，JAXA–RR–18–008，11 ～ 20，宇宙航空研究開発機構（2019）(5) 宇宙航空研究開発機構・宇宙科学研究所、科学衛星運用・データ利用ユニット（C–SODA）：DataARchives and Transmission System（DARTS）https://www.darts.isas.jaxa.jp/執筆者紹介太田 聡2010 年入社。つくば事業部へ配属。現在まで、主にGNSS（Global Navigation Satellite System）や宇宙機軌道決定に関連する解析業務やシステム開発業務に従事。