Unscented Kalman Filterを用いた実時間軌道推定ソフトウェアの開発及び試行

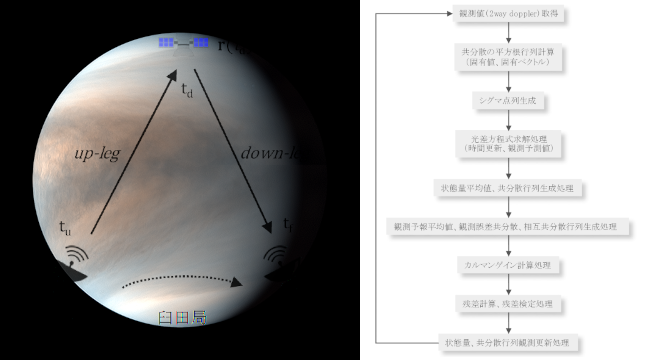
1 MSS技報・Vol.28＊つくば事業部 第二技術部
Unscented Kalman Filterを用いた実時間軌道推定ソフトウェアの開発及び試行
Development and trial of real－time trajectory estimation software using Unscented Kalman Filter
中嶋 憲＊　Ken Nakajima
　拡張カルマンフィルタ（EKF）は、非線形システムの状態推定アルゴリズムとして広く普及している。しかしながら、EKFはチューニングが難しく、システムの非線形性が強い場合には、しばしば信頼性の低い推定値を与えることがある。これは、EKFが線形化に依存して状態の平均及び共分散を伝搬することに起因している。　1990年代になると、EKFの線形化誤差を減少させるカルマンフィルタの拡張としてUnscentedKalman Filter（UKF）が提案され、現在では、EKFに替わる非線形システムの状態推定アルゴリズムとして利用されている。　MSSにおいても、宇宙航空研究開発機構（JAXA）からの委託業務として、UKFを用いた実時間軌道推定ソフトウェアを開発する機会があり、また、これをあかつきの金星軌道投入で試行し、その有効性を明らかにすることができた。以下では、開発した実時間軌道推定ソフトウェアのUKFアルゴリズムを説明し、あかつきでの試行結果を紹介する。
　The Extended Kalman Filter（EKF）is the most widely applied state estimation algorithm fornonlinear systems. However, the EKF can be difficult to tune and often unreliable estimation if thesystem nonlinearities are severe. This is because the EKF relies on linearization to propagate themean and covariance of the state.　In the late 1990's, Unscented Kalman Filter（UKF）was proposed as an extension of theKalman filter that reduces the linearization error of EKF, and is now used as a state estimationalgorithm for nonlinear systems replacing EKF.　We also had the opportunity to develop real－time trajectory estimation software using UKF as acommissioned work from the Japan Aerospace Exploration Agency（JAXA）, and tried it with theVenus orbit insertion of Akatsuki, and we were able to confirm the availability of UKF. In thefollowing, we will explain the UKF algorithm of the real－time trajectory estimation software wedeveloped and introduce the results of the trials at Akatsuki's Venus orbit insertion.
1．まえがき
　我々はこれまでにも静止軌道投入制御時の実時間軌道推定ソフトウェアをEKFで構築し、ETS－VI及びCOMETS等のアポジエンジン噴射時に利用した実績を持つ（1）。しかしながら、このソフトウェアはフィルタの安定性を確保するため３局からの同時観測（2way主局及び3way従局２局）を前提としていた。このため、このソフトウェアの利用には多くの観測資源が必要であることから、静止軌道投入制御時以外への利用に進展は見られなかった。このようなとき、EKFに内在する線形化誤差の問題を軽減し、上記の観測前提を緩和できる可能性を持つUnscented Kalman Filter（UKF）が登場した。我々は、このUKFを試すべくJAXAの下、その利用目的を新たにスペースデブリの1パス軌道推定、月惑星における実期間軌道推定に定め、UKFによる実時間軌道推定ソフトウェアを開発し、かぐや月周回軌道投入制御時軌道推定の事後評価（2）等を行い、2015年12月７日のあかつき金星軌道投入制御時に実時間で軌道推定（3）を試行し、その有効性を確認することができた。　以下では、開発した月惑星対応UKF実時間軌道推定ソフトウェアのアルゴリズム及びあかつきでの試行結果2 MSS技報・Vol.28（9）（10）となり、状態ベクトルと共分散行列には直接的な関連性がないため、共分散行列内に状態ベクトルが存在する保証はなく、非線形性が厳しいシステムでは、フィルタが偽収束する場合がある。また、式（10）では前回値を引き継いでいることから、共分散行列の非負定値対称性が崩れ易く、フィルタを不安定にする要因となる（一方、式（8）は時間更新毎に正定値対称性が保たれる）。逆に計算コストにおいては、式（6）では（　　　）個のシグマ点列を数値積分することになり、EKFの（　　　）倍を要する。＜STEP3＞ 更新後シグマ点列による観測ベクトル、共分散行列及び相互共分散行列（11）（12）（13）（14）＜STEP4＞ 観測残差及び残差検定（15）のとき棄却　　　　　 （16）　ここで 　　は時刻（　 ）での観測値を、　　は棄却　値レベル、添え字（ ）は観測値（ ）に対応する要素を表す。＜STEP5＞ カルマンゲイン（17）＜STEP6＞ 状態ベクトル及び共分散行列の観測更新（18）（19）　以上が、一般的なUKFアルゴリズムとなる。2.2　平方根行列　式（3）の平方根行列は、通常コレスキー分解で算出するが、実装においては、共分散行列の固有値（正定値対称行列の固有値は全て正）及び固有ベクトルを求め、平方根行列を算出する（5）（6）。このとき式（3）は次のように表される。（3a）値及び固有ベクトルは、特異値分解あるいはヤコビ法により求めることができる。なお、実装ではヤコビ法で固有値及び固有ベクトルを算出している。　このように固有値及び固有ベクトルを求めることで、（20）について報告する。2．実時間軌道推定アルゴリズム2.1　UKFアルゴリズム　UKFの特徴は、モンテカルロ手法のようにシグマ点列と呼ばれる確率分布に従って発生させたサンプル点に対し非線形変換し、変換された後の点列についてサンプル平均をとることで、状態ベクトルの条件つき期待値、共分散行列を算出する（Unscented Transformation）ところにある。このためEKFのようなヤコビ行列の計算を必要としないことも大きな特徴となる。　以下の離散時間状態空間モデル（1）（2）を考える。ここで、 、 、 は、それぞれ状態ベクトル、制御ベクトル、観測ベクトルであり、　、　は非線形関数である。また、　　　　、　　　　は、平均０、共分散行列がそれぞれ　、　のガウス白色雑音とする。なお、状態ベクトルとその共分散行列の初期値　、　は与えられているものとする。このとき、離散時間　から　　における（以下、離散時間は添え字　、　　　で表すものとする）UKFのアルゴリズムは、以下のステップで構成される。＜STEP1＞ シグマ点列　及び重み係数　 の計算（3）（4）（5）　ここで、　は状態ベクトルの平均、　　　は共分散行列　の平方根行列の第 列ベクトル、　は対象システム毎の調整パラメータを表す。この平方根行列は、コレスキー分解を用いて計算することが最も簡易な方法となるが、本ソフトウェアの実装においては、2.2節に示す方法で算出している。なお、シグマ点列及び対応した重み係数の与え方については、上記以外の方法もある（4）。＜STEP2＞ シグマ点列及び共分散行列の時間更新（6）（7）（8）　EKFの場合、式（6）（7）（8）は、　ここで　 は固有値、　　は固有ベクトルを表す。固有3 MSS技報・Vol.28　推定パラメータは、探査機位置・速度ベクトルに上記推力加速度誤差（変動）ベクトルを加えた９個の状態量とする。従って、式（3a）におけるシグマ点列は最大19点（　，　 ，　 は計画された制御開始時刻から推定を開始）となる。　また、探査機位置・速度ベクトルの基準座標系は、太陽系重心天文座標系（Barycentric Celestial ReferenceSystem，BCRS）、基準時系は、太陽系重心力学時（Barycentric Dynamical Time，TDB）を採用し、各座標系間、各時系間の変換は、IERS2010（8）に準拠している（金星中心回転固定座標系と慣性座標系間の変換は、参考文献（9）に準拠）。　式（21）運動方程式の数値積分（式（6）に相当）は、ドルマン－プリンス法に基づく刻み幅可変の８次陽的ルンゲ－クッタ法（10）を利用している。2.4　観測モデル　あかつきは臼田局からの2wayドップラーで観測される。我々は、これをデルタレンジの時間変化率としてモデル化した。2wayドップラーの計測インターバルを　、　番目の計測タイムタグを　、探査機位置・速度ベクトルを 、　、地上局位置・速度ベクトルを　、　とし、光差方程式を求める関数を とすれば、2wayドップラーのdown－legにおける探査機送信時刻　は式（23）で表される。ここで　は地上局受信時刻（　　　　 ）。次に、この探査機送信時刻　からup－legにおける地上局送信時刻　を式（24）から求める。これより受信時刻（ 　　　　）のレンジ　　　は式（25）となる。（23）（24）（25）　同様に受信時刻　　　　　 　に対するレンジ　　　を求めれば、デルタレンジ　及び距離変化率　は、（26）（27）から求めることができる（図１参照）。式（23）のdownlegを例に関数 を説明する。関数 では式（28）の光差方程式を満足する　を繰り返し計算（ニュートン－ラプソン法）により求める。繰り返し計算の過程における　　 、　　　は、都度2.3節に示した運動方程式の数値積分により計算する。（28）　ここで、式（28）の右辺第２項は太陽重力（　）によとなる成分を除き、状態ベクトル及び共分散行列を再構成し、計算コストを低減することができる。　また、実装では数値安定性のため、式（8）（13）（14）を、（8a）（13a）（14a）として計算している。2.3　運動モデル及び推定パラメータ　式（21）に式（6）に供するあかつきの運動方程式を示す。（21）（22）　ここで、 　　　は太陽輻射圧による加速度ベクトル、　　　　はポストニュートン近似の多体問題による加速度ベクトル（7（） エフェメリスはDE432を利用）、　　　は金星の非球対称成分（MGNP180Uポテンシャル係数を利用）による加速度ベクトル、　　　は金星軌道投入時計画推力加速度ベクトル、　　　は推力加速度の計画値で、推力及び比推力の係数テーブル（５次の多項式近似係数）と初期探査機質量から、事前に自動生成した計画推力加速度近似係数（同じく５次の多項式近似係数）に基づき計算される（衛星質量、増速度も同様）。（　，　）は推力方向の赤経、赤緯計画値。（　，　 ，　 ）はそれぞれ推力加速度誤差、推力方向赤経誤差、推力方向赤緯誤差を表し推定パラメータとなる。　（　，　 ，　 ）は推力加速度誤差ベクトルを模擬しており、擬似データを用いた事前の解析結果から、早期燃焼停止への追従性にも優れた、区分的に一定な変動モデル（Piecewise－Constant）を採用した。本モデルは、推定サイクル毎に、変動ベクトル及びこれに対応した共分散行列の成分を初期化（変動ベクトルについては０、共分散に関しては相関０で対角成分のみ初期分散値を与える）し推定する。（upleg4 MSS技報・Vol.283．あかつき金星軌道投入における試行結果　あかつきへの適用結果については、既に参考文献（3）で詳細が報告されている。以下では、特にフィルタ動作の観点から試行結果を報告する。3.1　観測残差による評価　UKFによる実時間軌道推定実施時の地球、金星及び探査機の幾何学的関係を図４に示す（本図は参考文献（3）図２からの抜粋）。　図４から明らかなように、図中の赤いラインで示された金星軌道投入（Venus Orbit Insertion，VOI）制御区間と地球方向は、ほぼ直交する関係にあり、ドップラー計測の観測性は良くない状況であった。EKFの場合には、偽収束しやすい状況と言える。　このような状況下で、本ソフトウェアが正常に動作していたかを確認するため、観測残差を評価する。図５に推定区間における観測残差の時系列プロットを、図６に軌道投入制御開始前、制御区間、再開後の区間別残差分布を示す。　理想的には、観測残差の統計値とドップラー計測誤差の統計値が一致していれば、フィルタは正常に動作したことになる。通常、ドップラー観測量はバイアスを持たるシャピロ遅延を示している。2.5　フィルタモデル　ここでは、2.1節のUKFアルゴリズムに対する、2.3節及び2.4節で示したモデルの組み込み方、具体的には状態量の推定時刻について説明する。　通常、式（6）は、観測時刻に対応した固定の時刻へ時間更新される。本システムの場合は、2wayドップラーのdown－legにおける探査機送信時刻がこれに相当する。ところで、図２に示すようにUKFの場合には、計測タイムタグを固定しシグマ点列毎に2.4節の光差方程式を適用するため、それぞれ異なる探査機送信時刻となる。　このため、探査機送信時刻にも式（7）を適用し、これを観測更新時刻とする。（29）　結局、式（6）の時間更新を行うためには、光差方程式を解く必要があり、また、式（11）の観測予報値も光差方程式の解であり、光差方程式を求める過程に状態量の時間更新及び観測予報値算出が含まれることになる。図３に機能面から見たUKF処理フローを示す。図１　観測時刻の定義図２　シグマ点列における探査機送信時刻図３　UKF処理機能フロー5 MSS技報・Vol.28ないため、計測誤差の平均値は０、そのランダム誤差成分はガウシアン・ノイズと仮定できる（なお、本試行では、式（13）の　として　値1.0mm/sを設定）。図６軌道投入制御開始前の観測残差分布は、平均は0.01mm/s、標準偏差は1.0mm/s、かつ、この統計値から生成した実線の正規分布とも一致しており、フィルタ動作は非常に良好だったことがわかる。また、同図制御区間の残差分布は、平均が0.1mm/s、標準偏差が8.4mm/sと軌道投入制御開始前より劣化し正規分布からの逸脱も見られるが、観測残差に大きな偏りはなく、推力加速度誤差の推定も含めフィルタ動作は良好だったと言える。制御区間の推定が良好だったと判断するもう一つの根拠は、図５において、軌道投入制御終了直後から約50分間の推定中断（軌道制御後約10分間の観測中断、その後測距データが正常な2wayドップラーになるまで約40分間を要した）があったが、その推定再開直後から観測残差の特性が良好であった点があげられる（制御終了時点における推定状態量の信頼性が高かった）。図６再開後の観測残差分布（図５における観測終了近傍の観測残差は評価から除外）は制御前の観測残差分布とほぼ同様な傾向となっている。　以上、観測残差の評価から本ソフトウェアは正常に動作していたと判断できる。　但し、制御区間及び再開区間を通じ、観測残差の平均に微小ながら制御前と比較した場合、明らかに大きな偏り（バイアス）が認められる。これは、制御区間で生じた状態量（軌道）の推定誤差が以降そのまま残った状態となり、残差平均に偏りを生じさせたものと推測される（今回の観測条件下における性能限界とも言える）。3.2　推定結果表示画面　本ソフトウェアは、推定結果を逐次画面に表示する簡易的なWeb機能を有している。運用者はこの画面を通じて、現在の探査機軌道、達成増速度等の監視を行うことができる。参考として、あかつき運用時の画面キャプチャーを図７、図８に示す。　図７及び図８は、金星軌道投入制御後の情報を表示している。図７右側のプロットは観測残差であり、上段が推定結果に基づく残差、下段が軌道予報値に基づく残差（本ソフトウェアは、軌道初期値及び軌道制御計画から軌道予報値を生成する機能を持つ）を示しており、実際の探査機軌道が計画からずれたものであることがわか図４　推定時天体と探査機の幾何学的関係（参考文献⑶より）図５　時系列観測残差図６　区間別観測残差分布6 MSS技報・Vol.28る。図８右側のプロットは、下段が達成増速度量の履歴となり、青が計画値、赤が推定値を示しており、増速度量が計画値よりも大きかったことがわかる。　このように、本ソフトウェアの表示画面は、推定結果を計画値と共に表示することで、現在の状態を直感的に判断できるものとなっている。4．むすび　開発した実時間軌道推定ソフトウェアのUKFアルゴリズムについて説明し、これがあかつきの金星軌道投入において良好に動作し、UKFはEKFにかわりうる非線形システムの状態推定手法であることを報告した。　本ソフトウェアの適用範囲を広げるべく、現在も機能追加が進行中であり、スペースデブリや新たな深宇宙ミッションでの利用を目指し、JAXAと共に、将来的にはなくてはならないシステムへと成長させていきたい。　最後に、本ソフトウェアの開発に対し有益な技術的アドバイスを頂き、あかつきへの試行に際しては、事前解析及び実運用を実施頂いた、宇宙航空研究開発機構研究開発部門第一研究ユニットの関係者の皆様に深く感謝申し上げます。参考文献⑴ Ogawa，M.，Hirota，M.，Sawabe，M.，Nakajima，K.，Hotta，M.：NASDA'S Real Time TrajectoryEstimation Program（RTEP），SpaceflightDynamics Colloque 95，Toulouse France，CNES，887～895（1995）⑵ 中村 涼介，廣瀬 史子，池田 人，中嶋 憲：月惑星軌道における実時間軌道・制御量推定，第56回宇宙科学技術連合講演会（2012）⑶ 秋山 恭平，池田 人，杉本 洋平，能美 亜衣，廣瀬史子，中嶋 憲：リアルタイム軌道推定手法によるあかつき金星軌道投入精度の評価，第60回宇宙科学技術連合講演会（2015）⑷ Simon，D.：OPTIMAL STATE ESTIMATION，Wiley－Interscience（2006）⑸ Luo，X.，Moroz，I. M.：Ensemble Kalman filterwith the unscented transform，Physica D：Nonlinear Phenomena，238，No.5，549～562（2009）⑹ Luo，X.，Moroz，I. M.，Hoteit，I.：Scaled unscentedtransform Gaussian sum filter：theory andapplication，Physica D：Nonlinear Phenomena，239，No.10，684～701（2010）⑺ Moyer，T. D.：Mathematical Formulation of theDouble－Precision Orbit Determination Program（DPODP），NASA CR－118673（1971）⑻ Petit，G.，Luzum，B. eds.：IERS Conventions2010，IERS Conventions Centre⑼ Archinal，B. A. et al.：Report of the IAU WorkingGroup on Cartographic Coordinates and RotationalElements：2009，Celestial Mechanics andDynamical Astronomy⑽ ハイラー，E.，ネルセット，S. P.，ヴァンナー，G.：常微分方程式の数値解法Ⅰ，Springer執筆者紹介中嶋 憲1986年入社。東京事業所宇宙開発部（当時）へ配属。H－Iロケット誘導解析、月ミッション軌道解析に従事。つくば事業部異動後、追跡管制軌道力学系ソフトウェア開発、衛星測位解析等に従事。図７　推定値／観測残差プロット画面例図８　推定値／達成増速度プロット画面例