フリーソフトウェアScilab/Scicosによる数値計算

フリーソフトウェアScilab/Scicosによる数値計算
Numerical Computations with Scilab/Scicos
矢田部 学＊　
Manabu Yatabe
49 ＊鎌倉事業部 第一技術部技術論文
　数理モデルを開発する場合、その妥当性を数値計算により確認することが重要である。この際、数値計算に特化したツールを用いると効率的である。モデル検証のために、我々のグループは、多数の数学関数を備えているフリーソフトウェアのScliab/Scicosを使用している。本稿では、Scilab/Scicosによる２つの基本的な数値計算例について紹介する。
　In developing mathematical models, it is essential to confirm the validity of the formulations by numerical computations. Use of specialized software is effective for this purpose. To verify the mathematical models, members of our group have employed Scilab/Scicos, a free scientific software package having numerous mathematical functions. In this report, the author shows two basic numerical computations using Scilab/Scicos.
1．まえがき
　鎌倉事業部第一技術部では防衛関係のM&S（Modelingand Simulation）業務を行っている。M&S業務においては、基礎原理から新たにモデルを定式化したり、既存のモデルを考え直す作業が発生する。その場合、モデルの妥当性を数値計算により検証することが重要である。この目的のためには、豊富な数学関数やtoolboxを備えたMATLAB※1などの数値計算に特化したソフトウェアの利用が便利である。　しかし、複数の計算機を用いてグループで作業を行う場合、ライセンスの問題が発生する。このような場合には、フリーのソフトウェアの使用が考えられる。そのため、我々のグループではモデルの検証ツールとしてフリーソフトウェアのScilab/Scicosを用いている。　本稿では、数理モデルの検証に有用なScilab/Scicosによる数値計算について紹介する。
2．Scilab/Scicosとは
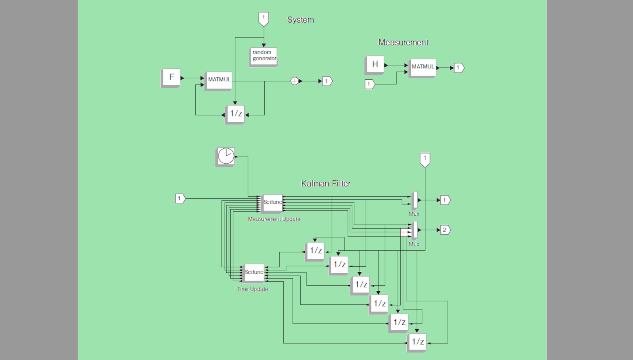
　Scilabは、フランスのINRIA（Institut national derecherche en informatique et en automatique、国立情報学自動制御研究所）とENPC（École nationale desponts et chaussées、国立土木学校）により開発された数値計算用のソフトウェアである。これは、線形代数、制御系、信号処理、グラフィック機能などに対応する命令や関数が豊富に用意されており、比較的簡単に数値計算プログラムを作成することが可能である。　また、ScicosはScilabに備えられているGUIを有するtoolboxで、この機能を用いるとブロック線図を用いて直截的にモデルを作りシミュレーションを行うことができる。これはMATLABのSimulink※1に類似している。　Scilab/ScicosはWindows、LinuxおよびMacOSに対応し、インターネット上からダウンロードして自由に使用することできる（http://www.scilab.org/）。　使用方法についてはWeb検索、一般の書籍（例えば⑴⑵⑶⑷）、およびScilabのHELP機能などから必要な情報を入手できる。　なお、2009年12月リリースのScilab5.2からScicosは、それを発展させたXcosに変更されている（http://www.scilab.org/products/xcos）。ただし、2010年７月時点では、古いバージョンのScilab/Scicosもダウンロード可能である。3．数値計算例　Scilabによる数値計算のプログラムとScicosのプロック線図によるシミュレーションの例を紹介する。ここでは、2007年10月にリリースされたScilab 4.1.2 およびScicos 4.2 を用いた。　数理モデルを開発する場合、その妥当性を数値計算により確認することが重要である。この際、数値計算に特化したツールを用いると効率的である。モデル検証のために、我々のグループは、多数の数学関数を備えているフリーソフトウェアのScliab/Scicosを使用している。本稿では、Scilab/Scicosによる２つの基本的な数値計算例について紹介する。　In developing mathematical models, it is essential to confirm the validity of the formulations bynumerical computations. Use of specialized software is effective for this purpose. To verify themathematical models, members of our group have employed Scilab/Scicos, a free scientificsoftware package having numerous mathematical functions. In this report, the author shows twobasic numerical computations using Scilab/Scicos.フリーソフトウェアScilab/Scicosによる数値計算Numerical Computations with Scilab/Scicos矢田部 学＊　Manabu Yatabe※１　MATLAB、Simulinkは、米国The MathWorks社の　　　登録商標である。MSS技報・Vol.21 50　式⑴は、とおくことにより、１階の連立微分方程式　⑵となり、Runge－Kutta法が適用できる。この解法に従ったScilabのプログラムを図２に示す。ここで、Runge－Kutta法のメイン処理が関数rk4であり、微分方程式の定義が関数diffEqsである。この例に示すように、Scilabはベクトルや行列を直接取り扱うことができるために、成分ごとの処理をする必要がなくプログラムが簡潔になる。ただし、Scilabでは、関数rk4で使用するユーザー定義の関数diffEqsを命令getfにより、使用前にロードする必要がある（図２参照）。これはMATLABなどとは異なる。　このプログラムを実行した結果を図３に示す。これより、変位（赤）と速度（青）が時間とともに減衰して行く様子が分かる。なお、ここでは次のパラメータを設定した。3.1　Scilabによるプログラミング　図１のような弾性定数のバネ、減衰定数のダンパー、および質量の質点よりなる系を考える。この系には、変位に比例する力と速度に比例する力が作用するので、運動方程式は　⑴と表される。ただし、およびとおいた。また、ドットは時間微分を表す。　この方程式の解を数値計算により求める。Scilabには、常微分方程式を解く関数odeが用意されているが、プログラム例を示すという目的から、ここでは敢えて４次のRunge－Kutta法⑷⑸によるプログラムを作成する。図１　減衰振動モデル図２　Runge－Kutta法のプログラム例function [ ] = rk4( )//　４次のRunge-Kutta法で//　微分方程式dx/dt=f(x,t)を初期条件(x0,t0)で解くgetf ('diffEqs.sci'); 微分方程式を定義した関数のロードglobal omg2 gmm;omg2 = 2.0; // ばね定数/質量gmm = 0.2; // 減衰定数/質量x = [0; sqrt(omg2)]; // 初期条件tmax = 30; // 評価終了時刻dt = 0.1; // 積分刻みi = 1;T(i,1) = 0; // 初期時刻 ⇒ T(1,1)X(i,1) = x(1); X(i,2) = x(2); // 初期値 x ⇒ X(1,:)for t = dt: dt: tmax[k1] = dt*diffEqs(t,x);[k2] = dt*diffEqs(t+dt/2,x+k1/2);[k3] = dt*diffEqs(t+dt/2,x+k2/2);[k4] = dt*diffEqs(t+dt,x+k3);x = x+(k1+2*k2+2*k3+k4)/6;i = i+1;T(i,1) = t; X(i,1) = x(1); X(i,2) = x(2); // プロット用データend// 結果のプロットclf( );plot2d(T,X);xset("font size",3);xtitle("Dampling Oscillation","Time","Displacement & Velocity");endfunctionRunge-Kutta法の処理関数rk4（Runge-Kutta法の処理） 関数diffEqs（微分方程式の定義）function [xdot] = diffEqs(t,x);// 減衰振動の微分方程式A = [ 0 1; -omg2－2*gmm];xdot = A*x;endfunction微分方程式Runge-Kutta法⇔51技術論文として　⑷と書ける。ただし、　である。いまの場合、とはスカラー量であるが、一般性を持たせるためベクトル的にボールド体で表記した。　式⑶と式⑷で表されるシステムについてのKalmanフィルター処理は以下のとおりである（例えば⑹⑺⑻⑼⑽などを参照）。　 ⑸　　ここで、式⑶と式⑷で述べた記号以外の新たなものは（Kalmanゲイン）、（推定誤差の共分散行列）、（システムノイズの共分散行列）、および（観測ノイズの共分散行列）である。上付き添え字は転置行列、－１は逆行列を意味する。　また、推定値であることを強調するために状態ベクトルにハットをつけ、状態ベクトルと共分散行列については観測更新前の値を（－）、観測更新後の値を（+）をつけて区別した。　以上に基づいてKalmanフィルターのシミュレーションを行う。このときのScicosのブロック線図を図５に示す。このブロック線図の意味は次のとおりである。左から右に眺めると、先ず、（I）システムの信号が生成（System）され、（II）それを測定（Measurement）して、（III）Kalmanフィルター処理（Kalman Filter）を行う。　ここで、図５の各処理ブロック（System、Measurement、Kalman Filter）はユーザー定義のブロックであり、図６に示すブロック線図をSuper Block機能を用い3.2　Scicosによるシミュレーション　Scicosのブロック線図を用いたシミュレーションの例として、図１に述べた減衰振動のシステムの変位を測定して、その時点の変位と速度を推定するKalmanフィルターを考える（図４）。ただし、システムはモデル化で考慮されていない擾乱を考慮するためにシステムノイズが加わるものとする。これは測定時の観測ノイズとは異なるものである。　図４の系にKalmanフィルターのアルゴリズムを適用するための定式化について述べる。式⑵より　である。この解は、時刻における状態ベクトルを、時間刻みをとして、離散的に考えると　と書ける。ここで、　　を遷移行列とする。ただし、は２×２単位行列である。このとき、状態方程式は、擾乱（システムノイズ）を考慮して　 ⑶と表される。　他方、測定については変位しか観測できないとすると、時刻における観測方程式は、観測ノイズを図４　Kalmanフィルター推定のイメージ1.51.00.50.0－0.5－1.0－1.50 5 10 15 20 25 30DisplacementVelocityTime（s）Damped OscillationDisplacemen（t m）/ Velocit（y m/s）図３　プログラムの実行結果システム測定観測ノイズ変位 を観測システムノイズKalmanフィルター変位 と速度を推定はね定数/質量：減衰定数/質量：初期変位　　：初期速度　　：MSS技報・Vol.21 52SystemNoiseMeasurement Kalman FilterKalman Filter Simulationrandomgeneratorwrite tooutput file図５　ScicosによるKalmanフィルターシミュレーションF1/z1/z1/z1/z1/z1/z1/zMATMULH MATMULScifuncMeasurement UpdateScifuncrandomgenerator1 System111 121MeasurementKalman Filter1Time UpdateMuxMux図６　Super Blockの中で定義したブロック線図53技術論文4．むすび　本稿では、M&S業務で数理モデルの検証に利用しているフリーソフトウェアのScilab/Scicosの数値計算例について紹介した。てグループ化したものである。図６において、Systemは減衰振動の力学系にシステムノイズが加わった式⑶の処理である。Measurementは式⑷で表される測定装置を模擬する。Kalman Filterは式⑸のKalmanフィルター処理のブロックである。　更に、Kalman Filterでは観測更新（MeasurementUpdate）と時間更新（Time Update）に対してユーザーが任意に処理を定義できる関数Scifuncを用いている。この処理はScilabのスクリプト言語で記述される（図７参照）。これらは式⑸に示した処理である。　図５に示したブロック線図によるシミュレーション結果を図８に示す。図の上段は変位の観測値であり、下段はこの観測値に基づいてKalmanフィルターで推定した変位（赤）と速度（青）である。ここでは、比較のために減衰振動の理論値（システムノイズ無し、黒破線）を重ね描きしている。変位と速度の真の初期値（0，1.41）から大きく離れたアプオリな初期値（5，5）から推定を開始したにもかかわらず、Kalmanフィルターが変位と速度を推定していることが分かる。　なお、このシミュレーションで設定したパラメータは以下のとおりである。Time（s）MeasurementDisplacement（m）Kalman Filter EstimationDisplacement（m）/Velocity（m/s）1.51.086420－2－4－60.50.0－0.5－1.0－1.50 5 10 15 20 25 30Time（s）0 5 10 15 20 25 30DisplacementVelocity図８　Kalmanフィルターシミュレーションの実行結果Scifunc (Measurement Update)time = u1; Y = u2;Xm(1) = u3; Xm(2) = u4;Pm(1,1) = u5; Pm(1,2) = u6; Pm(2,1) = u7; Pm(2,2) = u8;if modulo(time,dt_obs) <= 1e-5 thenK = Pm*H'*inv(H*Pm*H'+R);Xp = Xm+K*(Y-H*Xm);Pp = (eye(2,2)-K*H)*Pm;elseXp = Xm;Pp = Pm;endy1 = Xp(1); y2 = Xp(2);　y3 = Pp(1,1); y4 = Pp(1,2); y5 = Pp(2,1); y6 = Pp(2,2);Scifunc (Time Update)Xp(1) = u1; Xp(2) = u2;Pp(1,1) = u3; Pp(1,2) = u4; Pp(2,1) = u5; Pp(2,2) = u6;Xm = F*Xp;Pm = F*Pp*F'+Q;y1 = Xm(1); y2 = Xm(2);y3 = Pm(1,1); y4 = Pm(1,2); y5 = Pm(2,1); y6 = Pm(2,2);図７　Scifuncの記述例システム　ばね定数/質量　減衰定数/質量　初期変位　初期速度　システムノイズ測定　観測間隔　観測ノイズKalmanフィルター　状態ベクトルの初期値　誤差共分散行列の初期値　システムノイズの共分散行列　観測ノイズの共分散行列MSS技報・Vol.21 54⑹　Gelb, A.：Applied Optimal Estimation, MIT Press,1974⑺　片山　徹：応用カルマンフィルタ、朝倉書店、1983⑻　Brown, R. and P. Hwang：Introduction to RandomSignals and Applied Kalman Filtering with MatlabExercises and Solutions, John Wiley & Sons, 1996⑼　Grewal, M. and A. Andrews：Kalman Filtering:Theory and Practice Using MATLAB, John Wiley& Sons, 2001⑽　西山　清：最適フィルタリング、培風館、2001　これはフリーソフトウェアなので業務から離れて自己啓発のためにも使える。例えば、物理や工学などの理論を修得する際、身近な数値計算ツールとして利用すれば理解が深まる。興味を持たれた方は、Scilab/Scicosを試みられることをお勧めする。参考文献⑴　櫻井鉄也：MATLAB/Scilabで理解する数値計算、東京大学出版会、2003⑵　Campbell, S., J. Chancelier and R. Nikoukhah：Modeling and Simulation in Scilab/Scicos,Springer, 2006⑶　橋本洋志、石井千春：Scilab/Scicosで学ぶシミュレーションの基礎－自然・社会現象から、経済・金融、システム制御まで，オーム社、2008⑷　川田昌克：Scilabで学ぶわかりやすい数値計算法、森北出版、2008⑸　Woan, G.：The Cambridge Handbook of PhysicsFormulas, Cambridge Univ. Press, 2000