テクノロジー
技術レポート:アーカイブ
Category:ロケット・宇宙機・人工衛星開発
MATLABによるクォータニオン数値計算
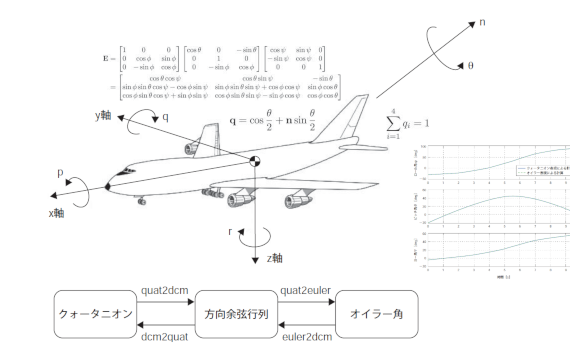
クォータニオンは、航空機などでよく用いられるオイラー角のように角速度ベクトルとの関係が非線形で特異点をもつようなことはないため、飛行数値シミュレーションでは有用な回転表現である。
一般に、オイラー角の微分方程式を解く数値シミュレーションにおいては、特異点に落ち込んでしまい、数値解が発散してしまう。
クォータニオンについては昨年度技報で「クォータニオン計算便利ノート」として鎌倉事業部矢田部より報告がなされている。本書では、この資料をもとにクォータニオン表現による剛体の運動、およびオイラー表現による剛体の運動をそれぞれ実際にMATLABで実装、数値計算を行い、両回転表現の比較について報告する。
参考情報:
MATLAB によるクォータニオン数値計算 宍戸 幹夫* Mikio Shishido クォータニオンは、航空機などでよく用いられるオイラー角のように角速度ベクトルとの関係が非線形で特異点をもつようなことはないため、飛行数値シミュレーションでは有用な回転表現である。一般に、オイラー角の微分方程式を解く数値シミュレーションにおいては、特異点に落ち込んでしまい、数値解が発散してしまう。クォータニオンについては昨年度技報で「クォータニオン計算便利ノート」として鎌倉事業部矢田部より報告がなされている。本書では、この資料をもとにクォータニオン表現による剛体の運動、およびオイラー表現による剛体の運動をそれぞれ実際にMATLABで実装、数値計算を行い、両回転表現の比較について報告する。 The quaternion is a useful expression for rotation used in flight simulation. The relation between the quaternion and its angular rate is linear and the quaternion doesn’t have a singular point like Euler angles. Euler angles are often used to describe aircraft dynamics. Mr. Yatabe’s paper“Convenient note for calculating Quaternion”appeared in last year’s MSS Technical Report. In his paper, Mr. Yatabe summarized useful equations for attitude calculation using the quaternion. My paper compares quaternion and Euler angle expressions for rigid body dynamics. MATLAB is used to formulate and simulate rigid body dynamics as follow : 1.まえがき力学では、位置や姿勢角を時間微分することにより速度、角速度を得られるとは限らない。これは、位置や姿勢角を定義する座標系の移動、回転を考慮して時間微分を行わなければならないためである。このようなことを避けるため、位置ベクトルについては、座標系の移動、回転を考慮しなくて良い慣性空間上で定義されることが多い。しかし、姿勢角についてはこのようにはならず、航空機などで用いられるオイラー角では角速度ベクトルとの関係が非線形で特異点をもつ。そのため、オイラー角表現による飛行運動シミュレーションにおいては、上記特異点近傍で姿勢角が発散してしまう。オイラー角に変わる回転表現としてクォータニオンがある。クォータニオンは、回転軸と回転角よりなる4成分で3次元空間の回転を表現する。クォータニオンでは、オイラー角による回転表現で生じるような特異点が存在しない。そのため、航空機等の姿勢角表現に有効な方法である。そこで、本報告では、クォータニオン表現による回転表現を実際に数値計算が行えるようMATLABで実装および計算結果の確認を行い、そのプログラムソースコードを記載する。本報告による実装は、飛行機、ロケット、人工衛星等の運動シミュレーションや慣性装置、ジンバル機構を有するハードウエア等のモデリングとシミュレーションに適用できると考えられる。本報告は、まず取り扱う座標系と方向余弦行列の定義を行い、次に、オイラー角、クォータニオンの定式化について述べる。この定式化をもとに数値解析ツールであるMATLABで実装を行った後に数値計算結果を示す。2.座標系と方向余弦行列の定義本資料では、以下の2 つの座標系を取り扱う。・慣性座標系・機体座標系慣性座標系は、慣性空間に固定された座標系である。機体座標系は、航空機等の機体の重心位置に固定され、慣性空間を移動、回転する座標系である。両座標系とも右手系の直交座標系とする。機体座標系*鎌倉事業部 第三技術部 MSS技報・Vol.19 44技術解説MATLAB によるクォータニオン数値計算宍戸 幹夫*Mikio Shishidoクォータニオンは、航空機などでよく用いられるオイラー角のように角速度ベクトルとの関係が非線形で特異点をもつようなことはないため、飛行数値シミュレーションでは有用な回転表現である。一般に、オイラー角の微分方程式を解く数値シミュレーションにおいては、特異点に落ち込んでしまい、数値解が発散してしまう。クォータニオンについては昨年度技報で「クォータニオン計算便利ノート」として鎌倉事業部矢田部より報告がなされている。本書では、この資料をもとにクォータニオン表現による剛体の運動、およびオイラー表現による剛体の運動をそれぞれ実際にMATLABで実装、数値計算を行い、両回転表現の比較について報告する。The quaternion is a useful expression for rotation used in flight simulation. The relation between thequaternion and its angular rate is linear and the quaternion doesn’t have a singular point like Eulerangles. Euler angles are often used to describe aircraft dynamics.Mr. Yatabe’s paper“Convenient note for calculating Quaternion”appeared in last year’s MSSTechnical Report. In his paper, Mr. Yatabe summarized useful equations for attitude calculation usingthe quaternion. My paper compares quaternion and Euler angle expressions for rigid body dynamics.MATLAB is used to formulate and simulate rigid body dynamics as follow :では、軸を機体前方にとり、軸を下方にとることとする。機体座標系を図1に示す。航空力学では一般に機体座標系の軸をロール軸、軸をピッチ軸、軸をヨー軸と呼ぶ。方向余弦行列とは、任意の2つの座標系の関係を変換する行列である。本資料では、慣性座標系から機体座標系への変換行列を方向余弦行列とする。ここで、慣性座標系の基底ベクトルを、機体座標系の基底ベクトルをとすると、以下のような関係で表される。(1)3.オイラー角の定式化オイラー角は各軸まわりの回転角の組として定義され、方向余弦行列と同様に座標系の関係を表現する要素である。方向余弦行列が9つのパラメータからなるため剛体の回転を直感的に理解することは難しいが、オイラー角は3軸の回転角の組であるため回転を理解することは容易である。3.1 オイラー角表現による方向余弦行列慣性座標を, , 軸の順でそれぞれ, , 回転させたとき機体座標となる角をオイラー角とする。航空力学では, , 軸まわりの回転角をロール角、ピッチ角、ヨー角と呼ぶ。ここで、方向余弦行列はオイラー角を用い以下のように表わされる。(2)3.2 方向余弦行列からオイラー角表現式(2)より以下のように方向余弦行列を用いてオイラー角を定義することができる。(3a)(3b)(3c)3.3 オイラー角の微分方程式機体座標系での各軸の角速度をそれぞれ, , とすると、式(2)よりオイラー角の運動方程式は以下のように表わされる。(4a)(4b)(4c)上式のとおり、オイラー角の微分方程式はピッチ角の±90degに特異点が存在する。これが、オイラー角表現による姿勢角計算の欠点である。オイラー角による姿勢角計算を行う際は、特異点をさけるため、回転順序を変えてオイラー角を定義する等の工夫が必要である。4.クォータニオンの定式化クォータニオンは、回転軸と回転角よりなる4成分で3次元空間の回転を表現する。クォータニオンでは、オイラー角による回転表現で生じるような特異点が存在しない。そのため、飛行機等の姿勢角表現に有効な方法である。クォータニオンについて、「クォータニオン計算便利ノート」3)を参考に述べる。4.1 クォータニオンの定義クォータニオンは、回転方向の単位ベクトルと回転角の4成分で定義される。クォータニオンを図2に示す。(5)45技術解説y軸x軸z軸qpr図1 機体座標系の定義nθ図2 クォータニオンMSS技報・Vol.19 46ここで、クォータニオンの定義から明らかなとおりノルムは1である。(6)4.2 クォータニオン表現による方向余弦行列クォータニオン表現による慣性座標系から機体座標系への方向余弦行列は、以下のとおりである。(7)4.3 方向余弦行列からクォータニオン表現方向余弦行列からクォータニオンを求めるには、式(7)を用いる。まず、方向余弦行列の対角項からクォータニオンの1変数を求め、次に、求めた変数を用いてその他の変数を求める。対角項からを求めたときは、以下のとおりとなる。(8a)(8b)(8c)(8d)ただし、方向余弦行列の対角項からクォータニオンの1変数を選ぶ際は、変数がゼロにならないようなものにしなければならない。4.4 クォータニオンの微分方程式クォータニオンの時間微分は、角速度ベクトルを用いて以下のように表される。(9)上式のとおり、クォータニオンの微分方程式には、オイラー角では式(4)のように存在する特異点を持たない。5.MATLABによる実装5.1 MATLABとはMATLABは、データ解析、モデリング、シミュレーション、可視化などの数値解析、アルゴリズム開発に必要な統合開発環境を提供するアプリケーションソフトウエアである。さらに、制御系設計、信号処理、画像処理など各種分野に対して利便性の高い数値演算ライブラリがToolboxと呼ばれるMATLABを拡張するパッケージの形で提供されている。また、プログラミング言語として、効率的な数値解析プログラム開発を行う事も可能である。MATLABの特徴を以下に簡単に述べる。・データアクセスの容易性データの基本構造は行列であり、変数の型宣言や配列の大きさを宣言する必要がない。また行列を直接演算する事ができ、行列の一要素ごと演算する必要がない。・対話型操作環境とプログラミング機能統合開発環境により、コマンド実行、ファイル操作およびヘルプの参照などのオペレーションを対話形式で行える。また、MATLABはインタプリタ型式の言語であるため、コンパイル、リンクといったプログラムの作成および変更から実行するまでの手間が少ない。・豊富な数値計算関数とグラフィックス関数MATLABのみで800以上の関数、コマンドが提供されている。拡張パッケージであるToolboxにより、さらに関数、コマンドが提供されている。また、豊富なグラフィックス関数を用いることにより、容易に計算結果を可視化することができる。5.2 MATLABで作成した関数一覧数値計算を行うにあたって、MATLABで実際に作成した関数の一覧を表1に示す。また、クォータニオン、オイラー角、方向余弦行列の関係および作成した関数の関係を図3に示す。図3で示されるように、方向余弦行列を介して、クォータニオンとオイラー角の変換が可能である。次節以降で作成した各関数についての概要を説明する。5.3 方向余弦行列計算オイラー角から方向余弦行列を計算する関数euler2dcm のソースコードを図4に示す。この関数の表1 関数一覧関数処理内容図番号dcm=euler2dcm(euler) オイラー角から方向余弦行列を計算図4dcm=quat2dcm(q) クォータニオンから方向余弦行列を計算図5euler=dcm2eule(r dcm)方向余弦行列からオイラー角を計算 図6q=dcm2quat(dcm) 方向余弦行列からクォータニオンを計算図7dx=euler_eq(t,x) オイラー角の微分方程式を計算図8dx=quat_eq(t,x) クォータニオンの微分方程式を計算図9simdemo オイラー角とクォータニオンの比較計算図1047技術解説引数はオイラー角3要素をもつベクトルeulerであり、戻り値は方向余弦行列dcmである。計算式は、式(2)である。次に、クォータニオンから方向余弦行列を計算する関数quat2dcmのソースコードを図5に示す。この関数の引数はクォータニオン4要素をもつベクトルquatであり、戻り値は方向余弦行列dcmである。計算式は、式(7)である。5.4 方向余弦行列からオイラー角、クォータニオン計算方向余弦行列からオイラー角から計算する関数dcm2eulerのソースコードを図6に、クォータニオンから方向余弦行列を計算する関数dcm2quatのソースコードを図7に示す。これらは、式(3)、式(8)を実装したものである。ただし、dcm2quat 関数については、対角項から各クォータニオン変数を算出し、その中で最大となる変数を選んで、その他の変数を再計算している。5.5 微分方程式計算オイラー角の微分方程式を計算する関数euler_eqのソースコードを図8に示す。次に、クォータニオンの微分方程式を計算する関数quat_eqのソースコードを図9に示す。また、この微分方程式を実際に解く関数が図10で示されるsimdemoである。この関数は、MATLAB組み込み関数である常微分方程式のソルバode23を使用して両微分方程式を解いている。図4 eular2dcm 関数図5 quat2dcm 関数図6 dcm2euler 関数図7 dcm2quat 関数図8 euler_eq 関数クォータニオン方向余弦行列オイラー角quat2dcmdcm2quat euler2dcmquat2euler図3 クォータニオン、オイラー角および方向余弦行列の関係MSS技報・Vol.19 48図9 quat_eq 関数6.数値計算結果数値計算は、表2に示す2条件で行った。条件1として、特異点をとらない場合、オイラー角、クォータニオンによる両手法が一致することを確認する条件を選んだ。次に、条件2として、オイラー角が特異点をとる条件を選んだ。まず、条件1での数値計算結果を図11、12に示す。図11で示すクォータニオン表現による姿勢角は、クォータニオンを方向余弦行列に変換し、さらにオイラー角に変換したものである。条件1は、オイラー角が特異点による発散がない条件であるため、図11からわかるようにオイラー角、クォータニオンによる計算結果が一致する。オイラー角に変換する前のクォータニオンの各パラメータは図12を参照されたい。条件2での数値計算結果を図13、14に示す。条件2は、時間2sでオイラー角の特異点であるピッチ姿勢角が90degになる条件である。そのため、図13からわかるようにオイラー角による計算では、2sにロール姿勢角とヨー姿勢角が発散している。これに対してクォータニオンによる計算では、図14で示されるように発散せず良好な結果である。クォータニオンから変換したピッチ姿勢角が2s以降減少しているのは、方向余弦行列からオイラー角に変換する際に式(3)のとおりピッチ姿勢角の範囲が-90deg 90degとなるためである。ただし、クォータニオン自体に発散はないため問題ではない。図10 simdemo 関数表2 シミュレーション条件条件1 条件2初期ロール姿勢角-30deg 0deg初期ピッチ姿勢角-20deg 80deg初期ヨー姿勢角-10deg 0degロール角速度5deg/s 0deg/sピッチ角速度10deg/s 5deg/sヨー角速度15deg/s 0deg/s1005000 1 2 3 4 5 6 7 8 9 10-50ロール角φ[deg]60400 1 2 3 4 5 6 7 8 9 10-20200ピッチ角θ[deg]60400 1 2 3 4 5時間【s】6 7 8 9 10-20200ヨー角Ψ[deg]クォータニオン表現による計算オイラー表現による計算図11 条件1計算結果:オイラー角10-10 1 2 3 4 5 6 7 8 9 10q110-10 1 2 3 4 5 6 7 8 9 10q210-10 1 2 3 4 5 6 7 8 9 10q310-10 1 2 3 4 5 6 7 8 9 10q4時間【s】図12 条件1計算結果:クォータニオン参考文献盧James R. Wertz: Spacecraft Attitude Determination and Control, Kluwer Academic Publishers,1978.盪加藤寛一朗:航空機力学入門,東京大学出版会,1982.蘯矢田部学:クォータニオン計算便利ノート,MSS技報vol.18,2007.49技術解説ロール角φ[deg]2001000 1 2 3 4 5 6 7 8 9 10-2000-1002001000 1 2 3 4 5 6 7 8 9 10-2000-100ピッチ角θ[deg]2001000 1 2 3 4 5時間【s】6 7 8 9 10-2000-100ヨー角Ψ[deg]クォータニオン表現による計算オイラー表現による計算図13 条件2計算結果:オイラー角10-10 1 2 3 4 5 6 7 8 9 10q110-10 1 2 3 4 5 6 7 8 9 10q210-10 1 2 3 4 5 6 7 8 9 10q310-10 1 2 3 4 5 6 7 8 9 10q4時間【s】図14 条件2計算結果:クォータニオン7.むすび剛体の回転表現であるオイラー角とクォータニオンについて、定式化とMATLABによる実装および数値計算を行った。数値計算結果から、特異点をとらない飛行条件ではオイラー角とクォータニオンの両手法の結果が一致することを確認した。また、特異点をとる飛行条件においては、クォータニオンの優位性を確認した。これにより、クォータニオンが飛行数値シミュレーションで有用な回転表現であることを示せた。