微分値の高精度計算法

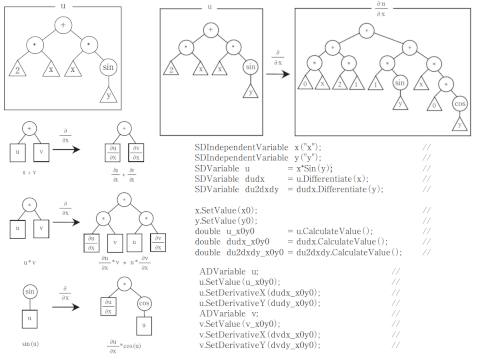
微分値の高精度計算法
24 ＊つくば事業部第一技術部技術論文微分値の高精度計算法High-Precision calculation methods for differential value林　健太郎＊ 小堀　壮彦＊Kentaro Hayashi, Takehiko Kobori
数値計算を行うプログラムにおいて微分値を計算する場合、数値微分では桁落ちによる精度劣化を招く。導関数をコード化するのは、独立変数の数や微分の階数が増えるほど誤りを生じやすい。これらの欠点を解消する方法として、記号微分と自動微分を紹介する。これらの方法を簡単に利用できるようにするため、適切なインタフェースを持つライブラリを作成することは意義がある。本稿では、記号微分による方法を試作したC++クラス･ライブラリについても述べる。
In the case of calculating differential values in a numerical calculation program, degradation ofprecision caused by cancellation often occurs. The more independent variables or higher differentialorder we have, the more mistakes we tend to make through coding derived functions. In order tosolve these problems, symbolic differentiation and automatic differentiation are introduced. It issignificant to make up some libraries which have appropriate interface to use these methods easily.This paper also refers to a prototype C++ class library of symbolic differentiation.
1．まえがきコンピュータは、もともと数値計算を高速に実行するために開発された機械であった。最初の高級言語であるFORTRANも、数値計算を用途として、計算したい数式を記述できるように仕様が決定された。現在では、世に出回るプログラムのうち、数値計算用のものは極めて少数となってしまった。コンピュータを用いて数値計算をさせる場合でも、MathematicaやMATLABなどの市販ツールを利用した方が便利なことが多い。しかし、大規模なシミュレーションや高速性が要求されるシミュレーション，あるいは高度な制御理論を応用したリアルタイム処理システムにおいては、数値計算プログラムの価値は失われていない。さて、数値計算の入門書では、関数の積分や常微分方程式の解法を必ず扱っているものであるが、微分値の計算について詳しく述べられているものは少ない。これは、次のような直感的な方法で間に合わせることが多いためである。盧数値微分：例えば、ある刻み幅での関数値の差分をその刻み幅で割る。盪独立変数の式として表された関数であれば、導関数をプログラムに書き込む。盧の数値微分は、いろいろ工夫はあるけれど、同程度の数値の差をとって小さい値で割ることに変わりはなく、桁落ちによる精度劣化は免れない。盪では、人手もしくは数式処理ツールによる計算により導関数を求め、それをプログラムに書き込む手間が必要であり、誤りも生じやすい。独立変数の数や微分の階数が多くなるほど、導関数を表す式は多く複雑になるため、その傾向は顕著となる。本稿では、これらの欠点を解消する微分値の計算方法として、記号微分による方法と自動微分による方法を紹介する。つまり、この２つの方法は、・桁落ちによる精度劣化を生じない。・導関数をプログラムに書き込む必要がない。という特長を持つ。もちろん方法自体はプログラムとして実装する必要があるが、微分値計算のユーザ自身が実装しなくてすむよう、適切なインタフェースを持つライブラリ化を行うことは可能である。2．記号微分2.1 記号微分の使用例記号微分（symbolic differentiation）（1）（2）とは、言わば数式処理による計算方法である。実際のコード例を示したほうがわかりやすいと思うので、まずは筆者らの試作したC++ によるクラス･ライブラリの使用例（図１）を示して説明する。このクラス･ライブラリの使用には、C++言語についての詳細を知る必要はない。C++は「Cよりも優れていMSS技報・Vol.18 25るC」（3）でもあり、オブジェクト指向技術に深く立ち入ることなく使用できる。（a）,（b）は、x, yが記号微分の独立変数であることの宣言である。（）内の文字列は、デバッグ用のものであり、本質的ではない。（c）でuは記号微分の変数であり、x*sin（y）と表せることを宣言する。SinはSDVariableを引数とし、SDVariableを戻り値とする関数である。また、多重定義した演算子*は、SDVariable同士の乗算を行う。独立変数も変数として扱えるよう、SDIndependentVariableからSDVariableへの暗黙の型変換を使用できるように設計しているので、（c）の右辺のように書くことができる。（d）は変数dudxが、uをxで偏微分したものであることの宣言である。DifferentiateはクラスSDVariableのメンバ関数であり、SDIndependentVariableを引数とする。（e）はさらにdudxをyで偏微分した変数をdu2dxdyと宣言していることを示す。（f）,（g）で独立変数x, yに対し、それぞれdouble型の値x0, y0を設定する。SetValue はクラスSDIndependentVariableのメンバ関数であり、doubleを引数とする。（h）～（j）で、クラスSDVariable のメンバ関数CalculateValue の戻り値として、x0, y0の値に応じた変数u, dudx, du2dxdy の値を得ることができる。つまり、u_x0y0, dudx_x0y0, du2dxdy_x0y0 にはそれぞれ, ， を計算した値が入る。u＝x*sin(y)の偏導関数,をコードとして記述しなくても、偏微分係数を計算することができるのである。2.2 記号微分のデータ構造とアルゴリズム本節では、試作した記号微分の設計結果として、そのデータ構造とアルゴリズムについて述べる。微分係数の値を精度よく計算することが目的なので、より簡単な数式に変形する簡約化などの本格的な数式処理を行うことは、設計では考慮していない。独立変数の式として表された変数に対し、その式を情報として付加しておく。式の情報は木構造として表現する。例えば、変数uが独立変数x, y によってu = 2*x +x*sin（y）と表せるとき、その構造は図２に示すように表現することができる。ここで、木構造の葉を三角形で、ノードを円で表している。図２からわかるように、木構造の葉には独立変数または定数が相当し、ノードには加法，乗法などの演算や関数が相当する。ノードは、演算や関数の引数の数だけの枝をもつ。独立変数に値が与えられたとき、付随した木構造に従って計算していけば、最終的にその変数の値を得ることができる。記号微分における微分操作とは、この木構造を別の木構造に変形することに他ならない。この変形の方法は、微分公式に応じて次のとおり再帰的に定めればよい。盧ノードにおいては、その演算や関数の微分に応じて変形する。図３にノードの変形の例を示す。四角形で囲まれた部分は、それより下（葉に近い部分）の木構造全体を表している。箱の中の微分記号は、その箱の中の木構造に対して微分操作による変形を施すことを意味している。盪葉における微分操作では、定数は全て定数０にSDIndependentVariable x（"x"）; //（a）SDIndependentVariable y（"y"）; //（b）SDVariable u = x*Sin（y）; //（c）SDVariable dudx = u.Differentiate（x）; //（d）SDVariable du2dxdy = dudx.Differentiate（y）; //（e）x.SetValue（x0）; //（f）y.SetValue（y0）; //（g）double u_x0y0 = u.CalculateValue（）; //（h）double dudx_x0y0 = dudx.CalculateValue（）; //（i）double du2dxdy_x0y0 = du2dxdy.CalculateValue（）; //（j）図１　試作したC＋＋クラス・ライブラリにおける記号微分の使用例*2 x sin*+yux図２　式２*x＋x*sin(y)の木構造*xu􀀬􀀬+sincosv*uxv􀀬􀀬*u v+u v+xu􀀬􀀬xv􀀬􀀬uxu􀀬􀀬*u􀀬x􀀬􀀬x􀀬􀀬x􀀬*cos (u)xu􀀬􀀬x* v u * vxu􀀬􀀬+􀀬􀀬xvxu􀀬􀀬+􀀬􀀬u * vsin (u)u + v図３　微分操作におけるノードの変形の例26技術論文置き換える。独立変数は、もしそれが微分する独立変数と一致していれば定数１に、そうでない場合は定数０に置き換える。これにより、例えば図２に示した木構造の微分操作による変形は、図４のように表される。このように偏微分して得られる変数においても、独立変数の式として表す情報を持っているので、その値を計算したり、再度微分したりすることができる。この設計では、変数ごとに独立変数の式を情報として持っているので、メモリの使用量が多い。図４に示すように、０を掛けられる式の情報など、無駄な情報も持っている。また、微分の計算では木構造を変形したり、値の計算ではいちいち独立変数の値まで戻って計算するなど、実行時間もかかる。改良の余地はあるが、数値微分や３章で示す自動微分など、他の微分値の計算方法に比べて、計算機資源を浪費することに変わりはない。しかしながら、プログラム中に書いた式を何度でも気軽に微分できるのが、記号微分の魅力である。数値計算プログラムにおいて、局所的に微分値の計算を組み込む必要がある場合に有用であろう。例えば、ちょっと込み入った式で表されるような、非線型方程式をNewton-Raphson法4）で解きたいとか、曲線や曲面の曲率を求めたいといった場合がその例である。3．自動微分3.1 自動微分の計算方法自動微分（automatic differentiation）（1）（6）（7）では、各変数について、その値と必要な階数までの微分値を組にしたデータとして扱う。つまり、加算や乗算などの演算やsin, cosなどの関数計算を行う場合には、その値だけでなく微分値まで計算するのである。したがって計算元の変数（例えば入力変数）に対しては、その値だけでなく必要とする階数までの微分値も設定する必要がある。以下、２変数の１階微分係数まで必要とする場合について簡単に述べる。例えば、変数u, v に対してu*v を計算するときは、次の（1）～（3）の左辺の値を全て計算し、その計算式は右辺による。（1）（2）（3）また、sin（u）を計算するときは、次の（4）～（6）の左辺の値を全て計算し、その計算式は右辺による。（4）（5）（6）自動微分においては、独立変数x, yやその値x0, y0を意識する必要はない。もちろん、独立変数を計算元として選択することは可能で、その場合は　　　　　　　　，とすればよい。ここで説明したのは、２階以上の微分係数は必要でない場合の方法である。より高階の微分係数まで要する場合は、演算や関数計算の各段階において、その階数までの微分値の計算を要する。高階の微分値の計算式は（2）,（3）,（5）,（6）のように簡単ではない。階数が高くなるほど、また独立変数の数が増えるほど、必要な微分係数の数も増え、微分値の計算は複雑になる。3.2 自動微分の使用例自動微分の使用例として、変数の数及び微分の階数をcosy0x **siny*+0 x 2 1* *++xu􀀬􀀬1*2 x sin*+yux􀀬x􀀬図４　図２に示した木構造の微分操作による変形MSS技報・Vol.18 27２変数、１階まで限定する場合について述べる。このように簡単な場合は、変数の値および１階微分係数の値をデータ･メンバとして持つクラス（図５のADVariable）を１つだけ作ればよい。演算や関数計算、例えば乗算やSin関数においては、式（1）～（3）や式（4）～（6）に基づいてデータ・メンバの値を計算する。使用例は図５のようになる。（a）はu が自動微分を行う変数であることの宣言である。（b）によりuの値としてdouble型のu_x0y0を設定する。（c）,（d）でuをそれぞれx, yで偏微分した微分係数としてdouble型のdudx_x0y0, dudy_x0y0を設定する。SetValue , SetDerivativeX , SetDerivativeYは、クラスADVariable のメンバ関数である。（e）～（h）で変数vについて同じことを行う。（i）で変数wが、u*sin（v）と表せることを宣言する。本節の例において実質的な微分値の計算を行うのは（i）の右辺だけである。多重定義した演算子* は、ADVariable同士の乗算として式（1）～（3）の計算を実行する。また、SinはADVariableを引数としADVariableを戻り値とする関数であり、式（4）～（6）の計算を実行する。（j）～（l）で、クラスADVariable のメンバ関数GetValue , GetDerivativeX , GetDerivativeY の戻り値として、wの値，wのxによる偏微分係数の値，wのyによる偏微分係数の値がそれぞれ得られる。ここで示した使用例では、独立変数の数と微分の階数を、それぞれ２と１に固定することを前提にしてクラスADVariableを設計した。独立変数の数と微分の階数を固定しない自動微分の設計も考えられるが、インタフェースに工夫が必要となると思われる。高階の微分値の計算も必要なため、実装も難しい。シミュレーションなどの計算量の多い数値計算では、計算機資源を浪費する記号微分よりも自動微分の方が有用である。利用方法としては、例えば、衛星の遷移軌道を消費推進薬がなるべく少なくなるように作成したい場合に適用できる、最適化問題（非線型計画法）が挙げられる。最適化問題の数値解法の多くは、目的関数および制約関数の独立変数に関する偏微分係数が必要であり、数値微分で間に合わせることもあるが、自動微分による偏微分係数を利用すれば、桁落ちによる精度劣化の悪影響を避けることができる。自動微分の計算を高速化するための発展的な方法として、関数値を計算するプログラムから偏導関数の値を計算するプログラムを生成することも行われている（8）（9）。「自動微分」、"automatic differentiation" でインターネット上を検索すれば、本稿より詳しい情報が得られるので、興味を持った方はお試しになられたい。4．むすび桁落ちによる精度劣化を生じない微分値の計算方法として、記号微分による方法と自動微分による方法を紹介した。記号微分や自動微分のように、数式に付随して有益な情報を付け加えていく方法は、数値計算プログラムの新しい可能性を示すものである。このような方法として、他には「精度保証つき数値計算」（1）（あるいは「数値計算の品質保証」（9））がある。これらの方法では、図１のSDVariableや図５のADVariableのように、組み込み型でないクラスを使用する。このようなユーザ定義型クラスに対しても、図１の（c）や図５の（i）のように計算したい数式になるべく沿って書けることが、プログラムの可読性を高めるために重要である。したがって、これらの方法を実装するプログラム言語としては、演算子の多重定義を利用できる方が有利である。参考文献・参考サイト盧計算機で微分方程式の厳密解を求める　大石進一http://www.sci.waseda.ac.jp/journal/vol1/no1/oishi/oish00.htm盪記号数式処理　平野拓一h t t p : / / w w w - a n t e n n a . e e . t i t e c h . a c . j p /̃hira/hobby/symbolic/index.html蘯Bjarne Stroustrup著，長尾高弘訳「プログラミング言語C++ 第３版」アジソン･ウェスレイ･パブリッシャーズ･ジャパン，ISBN4-7561-1895-X, 1998,pp.51盻William H. Press, Saul A. Teukolsky, William T.Vetterling , Brian P. Flannery 著，丹慶勝市・奥村晴彦・佐藤俊郎・小林誠訳「NUMERICALADVariable u; //（a）u.SetValue（u_x0y0）; //（b）u.SetDerivativeX（dudx_x0y0）; //（c）u.SetDerivativeY（dudy_x0y0）; //（d）ADVariable v; //（e）v.SetValue（v_x0y0）; //（f）v.SetDerivativeX（dvdx_x0y0）; //（g）v.SetDerivativeY（dvdy_x0y0）; //（h）ADVariable w = u*Sin（v）; //（i）double w_x0y0 = w.GetValue（）; //（j）double dwdx_x0y0 = w.GetDerivativeX（）; //（k）double dwdy_x0y0 = w.GetDerivativeY（）; //（l）図５　自動微分の使用例28技術論文RECIPES in C ［日本語版］」，技術評論社，ISBN4-87408-560-1, 1993，pp.264眈同，pp.307眇M. Berz, "Differential Algebraic Description ofBeam Dynamics to Very High Order", ParticleAccelerators, Vol.24, pp.109-124, 1989眄Wikipediah t t p : / / e n . w i k i p e d i a . o r g / w i k i / A u t o m a t i c _differentiation眩久保田光一，伊理正夫共著「アルゴリズムの自動微分と応用」現代非線形科学シリーズ３，コロナ社ISBN4-339-02602-6, 1998眤福井義成，野寺隆志，久保田光一，戸川隼人著「新数値計算」インターネット時代の数学シリーズ２，共立出版，ISBN4-320-01641-6，1999，Part 3