2023年度 三菱電機ソフトウエア技術レポート
Iterated-UKFを用いた小天体に対する相対画像航法の提案及びフォボスへの適用例
1.まえがき
近年、宇宙探査のフロンティアは小惑星や惑星の衛星へと移行しつつある。これらの探査ミッションでは、探査機と目標天体との相対位置が極めて重要な情報となる。一般的な手法では、複数の航法カメラ画像やライダー(レーザー距離計)による計測データを基に相対位置を推定している(1)。しかしながら、これらの手法には問題点も存在する。画像は、探査機・太陽・目標天体(衛星の場合にはその主天体)の幾何学的配置による日陰・掩蔽の影響を受け、ライダーは近距離の相対位置でのみ利用可能という制約である。
仮に単一の画像から相対位置を推定できれば、上記の観測制約が緩和されることになり、有効な相対航法技術となる。既に、単一の画像から相対位置を推定する手法はいくつか存在するが、その多くは目標天体の詳細な地形情報を必要とする。しかしながら、地形の詳細は探査初期段階では得られない情報である。
そこで、我々は新たな相対航法技術として、事前の詳細情報が得易い目標天体の全体形状に基づく推定手法を提案する。この手法が有効であれば、特に撮像機会に制約の多い衛星探査初期段階における有効な相対航法技術となる。
現在、国立研究開発法人宇宙航空研究開発機構(JAXA)では火星の衛星であるフォボスの探査を目的とした火星衛星探査計画(MMX:Martian Moons eXploration)が進行している。将来、このミッションにおける実データを利用し、我々の新たな手法の有効性が確認できることを期待する。
本論文では、この新たな手法について詳細に解説し、フォボスの模擬画像を用いた適用例とその精度評価結果について報告する。これにより、今後の小惑星や衛星探査における航法技術の進化に寄与することを目指す。
2.問題定義
探査対象天体の一枚の撮像画像から得られる観測量は限られたものになる。我々はこの観測量として、小惑星Ryuguの探査に成功したHayabusa2を参考にした(1)。具体的には、画像を二値化(0,1)し、その重心座標を観測量とする。
観測画像サイズをN 列×M 行、画素座標を p(n,m),1≤n≤N,1≤m≤M とすれば、その重心座標Cは次式で表される。
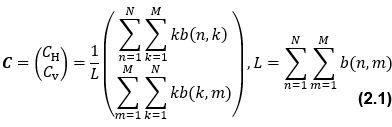
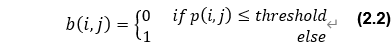
しかし、この観測量だけでは方向の情報しか含まれず、距離に関する情報を得ることができない。そこで、二値化した画像で1となるピクセル数の合計値Lも観測量として利用する。
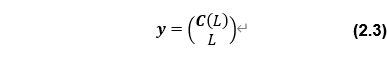
ところが、この方法ではそれぞれの観測量に相関関係があり非線形性が強く表れるという問題が生じる。また、太陽、主天体、その衛星の幾何学的配置による画像の陰影も、特に三軸が不等で地形が起伏に富む対象天体では、非線形性が強く表れる。このため、本問題に対して拡張カルマンフィルタ(EKF)を適用する場合、観測量に対する状態量のヤコビアンを定義することは容易ではない。そこで、我々はヤコビアンを不要とするアンセンテッド・カルマンフィルタ(UKF)(2)をこの問題に適用することにした。さらに、観測量の非線形性に対応するため、反復UKF(IUKF)の適用を考えた。
3.提案手法
3.1 IUKFアルゴリズム
この問題に対するIUKFアルゴリズムを以下に示す。同一慣性座標系における探査機初期位置誤差共分散行列をP0prb、探査対象天体の初期位置誤差共分散行列をP0obj、探査機と対象天体重心間の初期相対位置ベクトルをΔr0とする。このとき、撮像画像から得られる観測値(画像重心座標及び二値化ピクセル数)をyaとすれば、そのアルゴリズムは、
<初期状態量及び初期誤差共分散>
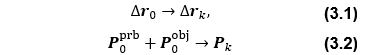
<コレスキー分解>
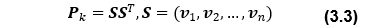
<シグマポイント>
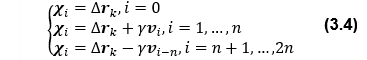
<平均観測量>
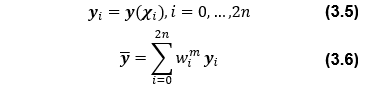
<観測誤差共分散>
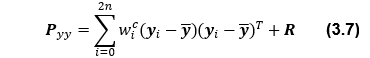
<相関誤差共分散>
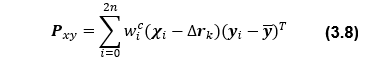
<カルマンゲイン>
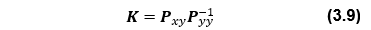
<推定状態量及び誤差共分散更新>
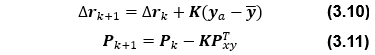
<収束判定>
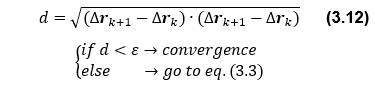
となる。ここで、SはPkをコレスキー分解した下三角行列、nは推定状態量数(この問題ではn=3)、Rは観測ノイズ誤差共分散、γ、wim及びwicは重み係数であり、それぞれ、
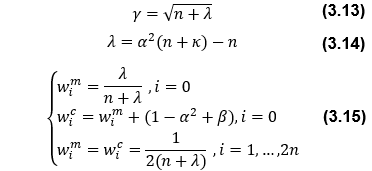
で与えられる(後述の解析においては、γ=1、β=2とし他のパラメータを調整)。
3.2 観測量計算
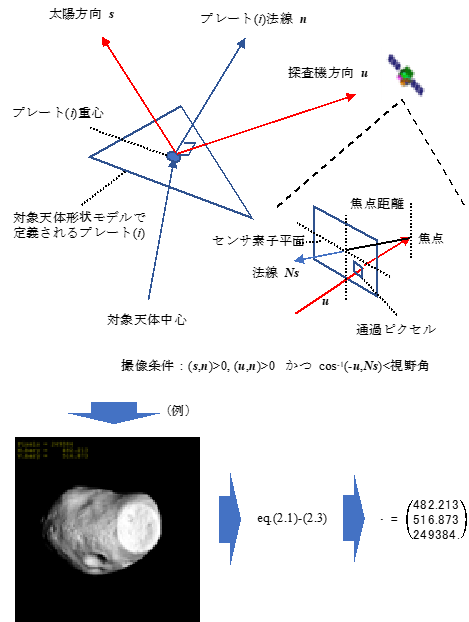
図 1 航法フィルタ内観測値生成概要
このアルゴリズムでは、適用する天体形状モデルの解像度に依存するが、式(3.5)における各シグマポイントの観測量生成計算が高負荷となる。具体的には、図1に示す対象天体形状を三角形プレートの集合で模擬した形状モデルと太陽及び探査機方向から可視・不可視を判断し、探査機姿勢、航法カメラの焦点距離及びセンサ素子サイズに基づき、画素平面上に対象天体のイメージを生成する。このとき、航法フィルタ内で生成する画像が視野範囲から逸脱することを避けるため、N×Mの領域を2倍に拡張している。これにより、シグマポイントにおける生成画像が視野範囲を逸脱した場合においても安定的な推定が可能となる。この航法フィルタ内生成画像から式(2.1)〜式(2.3)に基づき観測量を算出する。なお、天体形状モデルの処理に関しては、CSPICE API(3)を利用した。
4.精度評価
以下、本手法を火星衛星フォボスに適用し、主要誤差源が推定精度に与える影響を評価し、その有効性を確認する。
4.1 適用モデル及び誤差
本手法の推定精度に影響を及ぼす主要因として、次の誤差源が考えられる。
フォボスに関して
(ⅰ) 真の形状と航法フィルタ内形状モデルとの差異
(ⅱ) 真の自転と航法フィルタ内自転モデルとの差異
探査機に関して
(ⅲ) 真の姿勢と航法フィルタ内認識姿勢との差異
である。なお、探査機に起因する誤差源は直接的には画素平面の座標誤差であるが、探査機姿勢誤差に全て含まれるものとする。
(1) フォボス形状及び自転
表 1 フォボス形状及び自転モデル
| 対象 | モデル | 備考 |
|---|---|---|
| 形状 | GASKELL(GAS)(4) | 構成プレート数 3145728 |
| DLR(5) | 構成プレート数 274874 | |
| 自転 | IAU_2009(6) |
|
| IAU_2015(7) | 修正版 |
フォボスに起因する誤差源を解析に反映するため、2つの異なるモデルを採用する。一方は、真の撮像画像を模擬する形状モデルと自転モデル、もう一方は航法フィルタ内で適用する形状モデルと自転モデルとなる。解析に適用するフォボス形状モデルと自転モデルを表1に示す。
モデル間の相違を見るため、DLR形状モデルの表面上にGAS-DLRの差(半径差)を表示したものを図2に、自転モデルについては同一時刻における極軸方向の角度差及び緯経度ゼロ方向の角度差を図3に示す。なお、図2において赤の部分はGASに比較しDLRの半径が長い箇所を、青の部分はその逆を表している(スケール的に判別できないが線分長が半径差を示している)。
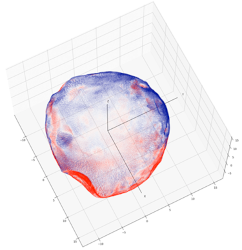
図 2 適用形状モデル間の相違
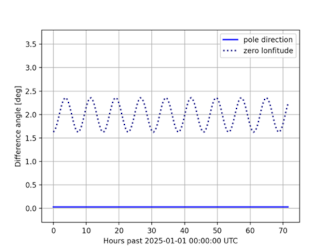
図 3 適用自転モデル間の相違
IAU_2009とIAU_2015の差は、極軸方向にはほとんどなく、経度方向に約2°の差(変動周期は自転周期の7.65時間)となっている。
(2) 探査機姿勢
慣性座標系とセンサ座標系との関係は次式でモデル化している。
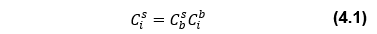
ここで、Cisは慣性系からセンサ座標系への変換行列、Cbs、Cibはそれぞれ機体座標系からセンサ座標系への変換行列、慣性系から機体座標系への変換行列を表している。ここに次式の誤差モデルを付加する。
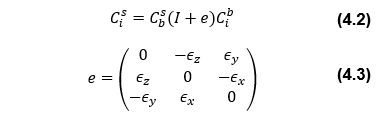
ここで、eが誤差を与える歪対称行列であり、各機体軸における姿勢誤差εx、εy、εzから構成する。センサ座標誤差を与える場合には、式(4.2)及び式(4.3)を適用する。誤差値は、εx、εy、εzそれぞれに対し0.1 degを想定する。
(3) フォボス天体暦
太陽及び火星の天体暦についてはDE430(8)を、フォボスの天体暦についてはmar097(9)を利用する。フォボスの天体暦位置誤差としては各軸1〜2kmを想定する。なお、この天体暦位置誤差は式(3.2)におけるP0objに相当している。
(4) 航法カメラ
航法カメラは表2に示すMMXに搭載されるWAC(Wide Area Camera)相当(10)を適用する。
表 2 航法カメラ特性
| 項目 | 特性値 |
|---|---|
| 水平方向画素数N | 1024 |
| 垂直方向画素数M | 1024 |
| 画角(全角) | 30° |
4.2 解析ケース
本解析の目的を踏まえ、表3に示す解析ケースを設定する。
表 3 解析ケース
| 識別及び目的 | モデル設定 |
|---|---|
| CASE1: 性能限界評価 |
実観測値模擬DLR + IAU_2009 フィルタ内モデルDLR + IAU_2009 姿勢誤差非考慮 |
| CASE2: 自転誤差影響評価 |
実観測値模擬DLR + IAU_2009 フィルタ内モデルDLR + IAU_2015 姿勢誤差非考慮 |
| CASE3: 形状誤差影響評価 |
実観測値模擬DLR + IAU_2009 フィルタ内モデルGAS + IAU_2009 姿勢誤差非考慮 |
| CASE4: 姿勢誤差影響評価 |
実観測値模擬DLR + IAU_2009 フィルタ内モデルDLR + IAU_2009 姿勢誤差考慮 |
上記ケースを表4に示す探査機-フォボス間距離及び日照条件を異とする複数の観測条件に対し実施する。ここで相対距離の下限値60kmは、表2に示した航法カメラでフォボスを撮影した場合、フォボスが視野範囲に収まる距離とした。仮に、視野範囲を逸脱している場合、観測残差をゼロとする複数の解が存在することになる。
表 4 観測条件
| 識別 | 相対距離 | 観測条件及び観測値 |
|---|---|---|
| OBS-1 | 60km | 図4(1)参照 |
| OBS-2 | 95km | 図4(2)参照 |
| OBS-3 | 195km | 図4(3)参照 |
| OBS-4 | 90km | 図4(4)参照 |
| OBS-5 | 100km | 図4(5)参照 |

図 4 観測条件・観測値
推定条件(全解析ケース共通)を表5に示す。表中、初期誤差共分散は、4.1節(2)記載の誤差と同等の誤差が探査機位置誤差にもあると仮定し、各軸3kmの位置誤差とした。
表 5:推定条件
| 項目 | 条件値 |
|---|---|
|
初期誤差共分散 式(3.2)相当 |
P0=diag[9.,9.,9.](km2) |
|
初期相対位置 式(3.1)相当 式(4.3)相当 |
<CASE4以外> Δr0=N(ΔrOBS-N,P0) ΔrOBS-Nは図4を参照 <CASE4> e =N(0,Pa) Pa=diag[0.01,0.01,0.01](deg2) |
|
観測ノイズ誤差 式(3.7)の R 相当 |
R =diag[σp2 , σp2 , σL2] σpは 0.5pixel σLは観測値Lの0.02% |
|
収束判定 式(3.12)の ε 相当 |
ε = 3 ( m ) イテレーション回数上限値 20 |
表3に示した各ケースそれぞれに対し表4に示した5つの観測条件下で推定精度を評価する。具体的には、表5に従い初期相対位置あるいは姿勢誤差を300組生成し、これらの推定結果を次式に示す統計量で評価する。
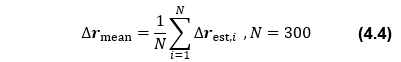
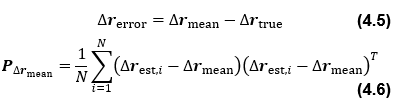
式(4.4)は収束点の平均値、式(4.6)はその平均値周りの収束点の分布特性を、式(4.5)は平均値と真値の差を表している。
4.3 解析結果
(1) CASE1(性能限界)
誤差非存在下における推定精度であり、表2に示した航法カメラ特性による本提案手法の性能限界を確認する。本結果を表6に示す。なお、以降に示す結果は、フォボス中心フォボス固定座標系IAU_2009を基準とし、errorは式(4.5)、sigmaは式(4.6)の各対角成分の平方根を表している。
表 6 CASE1精度評価
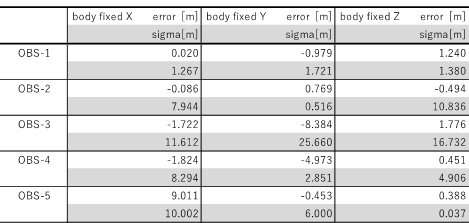
誤差非存在下における推定精度は、天体の解像度に関係し相対距離の影響が支配的となる。相対距離100kmで収束点の平均値回りに10m、200kmで30mの推定分散となっている。また、収束点平均値と真値との差についても分散と同等レベルであり、本提案手法が相対航法フィルタとして有効に機能していることが確認できる。参考として図5にOBS-1において初期相対位置誤差が最も大きいケースの推定過程を示す。
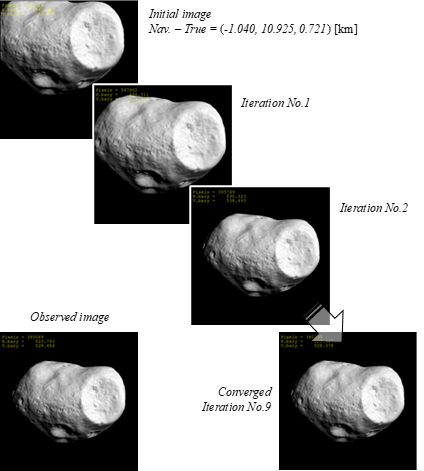
図 5 推定過程
(2) CASE2、CASE3(自転及び形状モデル誤差)
表7に自転モデル間の差に起因する推定精度を、表8に形状モデル間の差に起因する推定精度を示す。
表 7 CASE2精度評価
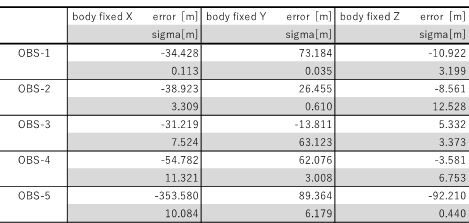
表 8 CASE3精度評価
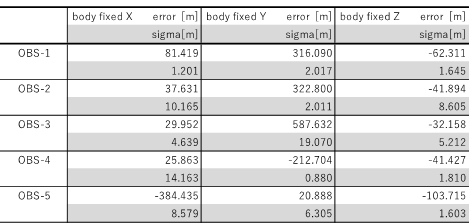
ここで特出すべき点は、平均値周りの推定分散が誤差非存在下における同分散と同じオーダであること、つまり、モデル誤差の影響により収束点の平均値は真値からずれるものの、その推定値はほぼ同じ点に収束しているところにある。したがって、対象天体に関連するモデルの精度が向上することで、この差は軽減される。
平均値と真値との差をモデル誤差に関連付け定量的に評価することは、撮像条件にも依存するため、現時点で明確な説明を与えることはできないが、フォボスに起因するモデル誤差の影響は、主に画像重心の誤差として現れている。その結果、表7の誤差は、図3に示された誤差2°×フォボス半径(平均半径を11kmとした場合、約380m)相当に、表8の誤差は、図2に示された誤差(最大±700m)相当となっている。
(3) CASE4(姿勢誤差の影響)
以上の解析では、対象天体に起因するモデル誤差が推定精度に与える影響について評価したが、ここでは探査機に起因する誤差、特に最も影響が大きいと考えられる姿勢誤差について評価する。具体的には、CASE1において、初期相対位置ではなく探査機姿勢に誤差を与え相対位置を推定することで収束点周りの分布を評価する。本結果を表9に示す。
表 9 姿勢誤差存在下精度評価
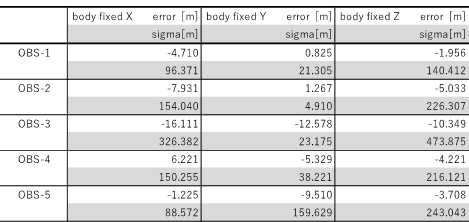
姿勢誤差は、対象天体に起因する誤差とは異なり、相対距離との相関が強く、かつ相対位置推定精度に大きく影響することがわかる。仮に、姿勢誤差による推定精度への影響をフォボスに起因する誤差の影響と同程度にするには、姿勢誤差も推定する等、何らかの工夫が必要になる。
最後に参考として、3.2節において言及した本手法の処理時間を表10に示す。
表 10 平均繰返し数及びCPU時間(*)

(*)ツールはC言語で実装し、Intel Core-i7 4GHz上で実行
5.むすび
本論文では、単一の対象天体画像から相対位置ベクトルを推定する手法としてIUKFを提案し、これを火星の衛星フォボスに適用することで、その有効性を示すことができた。推定値自体の誤差については、今後の対象天体に関連するモデルの改善が必要となるが、収束点周辺の分散については十分な精度が達成されている。しかしながら、探査機に起因する姿勢誤差については、その影響は大きく、実際の探査機姿勢精度では、満足な相対位置精度は得られない可能性がある。今後、探査機姿勢誤差も同時に推定する等、姿勢誤差を軽減する手法の検討を行う必要がある。具体的には、今回の解析結果を踏まえ、最初に姿勢誤差のみを推定し、その後段で姿勢誤差推定結果を引き継ぎ、相対位置と姿勢誤差を同時推定する手法の有効性を評価し、実運用に資するための改善を進めることを予定している。
謝辞
本論文で提案した手法は、宇宙航空研究開発機構(JAXA)から業務委託を受けた相対航法手法の検討結果を基に発展させたものです。また、図4で示した観測条件は、JAXAから提供されたデータに基づいています。
上記委託業務に関連し有益な技術的アドバイスをいただくとともに、本論文の執筆とデータの利用について快く承諾いただいたJAXA池田人氏及び坂本拓史氏に深く感謝申し上げます。
参考文献
(1) Yamamoto,K.,et al.:Dynamic precise orbit determination of Hayabusa2 using laser altimeter (LIDAR) and image tracking data sets,Earth Planets Space,72,85(2020)
https://doi.org/10.1186/s40623-020-01213-2
(2) Wan,E.A.,Van Der Merwe,R.:The unscented Kalman filter for nonlinear estimation,Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium,153~158(2000)
https://doi.org/10.1109/ASSPCC.2000.882463
(3) NASA Navigational & Ancillary Information Facility:Digital Shape Kernel Subsystem (DSK)(2023)
https://naif.jpl.nasa.gov/pub/naif/toolkit_docs/Tutorials/pdf/individual_docs/37_dsk.pdf
(4) ESA SPICE Service:PHOBOS_M157_GAS_V01.BDS,Mars-Express SPICE Kernel Dataset
https://spiftp.esac.esa.int/data/SPICE/MARS-EXPRESS/kernels/dsk/
(5) ESA SPICE Service:PHOBOS_K275_DLR_V02.BDS,Mars-Express SPICE Kernel Dataset
https://spiftp.esac.esa.int/data/SPICE/MARS-EXPRESS/kernels/dsk/
(6) ESA SPICE Service:PCK00010.TPC,Mars-Express SPICE Kernel Dataset
https://spiftp.esac.esa.int/data/SPICE/MARS-EXPRESS/kernels/pck/
(7) Archinal,B.A.,et al.:Correction to: Report of the IAU Working Group on Cartographic Coordinates and Rotational Elements: 2015,Celest Mech Dyn Astr,131,61(2019)
https://doi.org/10.1007/s10569-019-9925-1
(8) NASA Navigational & Ancillary Information Facility:de430.bsp,Generic Kernels on NAIF
https://naif.jpl.nasa.gov/pub/naif/generic_kernels/spk/planets/
(9) ESA SPICE Service:MAR097.BSP,Mars-Express SPICE Kernel Dataset
https://spiftp.esac.esa.int/data/SPICE/MARS-EXPRESS/kernels/spk/
(10) 巳谷真司 他:火星衛星探査計画MMX航法誘導制御系の設計と検証,第64回宇科連,3D05,2020